
【题目】如图,正方体![]() 中,
中,![]() 为底面
为底面![]() 的中心,
的中心,![]() 为棱
为棱![]() 的中点,则下列结论中错误的是( )
的中点,则下列结论中错误的是( )
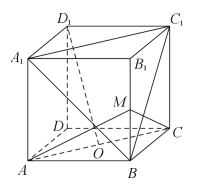
A.![]() 平面
平面![]() B.
B.![]() 平面
平面![]()
C.异面直线![]() 与
与![]() 所成角为
所成角为![]() D.
D.![]() 与底面所成角为
与底面所成角为![]()
【答案】D
【解析】
根据线面平行的判定定理可证明A正确;根据线面垂直的判定定理可证明B正确;易证![]() 并结合异面直线所成的角的定义可得C正确;根据过一点有且仅有一条直线与已知平面垂直可得D错误.
并结合异面直线所成的角的定义可得C正确;根据过一点有且仅有一条直线与已知平面垂直可得D错误.
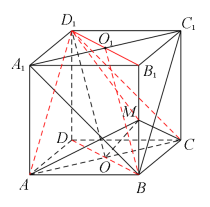
对A,连结![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点,连结
的中点,连结![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故A正确.
,故A正确.
对B,连结![]() ,
,![]() ,
,![]() ,设正方体
,设正方体![]() 的棱长为
的棱长为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
所以在![]() 中,
中,![]() ,所以
,所以![]() ,
,
又![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故B正确.
,故B正确.
对C,因为![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,所以
,所以![]() (或其补角)即为异面直线
(或其补角)即为异面直线![]() 与
与![]() 所成角,
所成角,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以异面直线![]() 与
与![]() 所成角为
所成角为![]() ,故C正确.
,故C正确.
对D,因为![]() 平面
平面![]() ,又过一点有且仅有一条直线与已知平面垂直,
,又过一点有且仅有一条直线与已知平面垂直,
故![]() 不与平面
不与平面![]() 垂直,故D错误.
垂直,故D错误.
故选:D


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
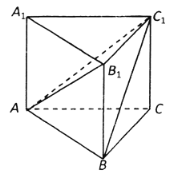
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
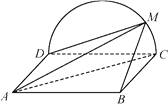
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
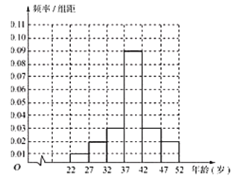
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
| |
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)对任意![]() ,
,![]() 都有恒成立,求实数a的取值范围;
都有恒成立,求实数a的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)当a=![]() 1时,求函数y=f(x)的单调区间;
1时,求函数y=f(x)的单调区间;
(2)求函数y=f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体质健康测试中,某辅导员随机抽取了12名学生的体质健康测试成绩做分析,得到这12名学生的测试成绩分别为87,87,98,86,78,86,88,52,86,90,65,72.

(1)请绘制这12名学生体质健康测试成绩的茎叶图,并指出该组数据的中位数;
(2)从抽取的12人中随机选取3人,记![]() 表示成绩不低于76分的学生人数,求
表示成绩不低于76分的学生人数,求![]() 的分布列及期望
的分布列及期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com