已知数列{an}中,a1=1,a2=2,且an+1=(1+q)an-qan-1(n≥2,q>0).
(1)设bn=an+1-an(n∈N*),证明:数列{bn}是等比数列;
(2)试求数列{an}的通项公式;
(3)若对任意大于1的正整数n,均有an>bn,求q的取值范围.
解:(1)由a
n+1=(1+q)a
n-qa
n-1(n≥2,q≠0)得,a
n+1-a
n=q(a
n-a
n-1),即b
n=qb
n-1(n≥2).
又b
1=a
2-a
1=1,q≠0,b
n≠0.
所以,{b
n}是首项为1,公比为q的等比数列
(2)由(1)有,b
n=q
n-1
又a
n-a
1=(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)=1+q+…+q
n-2(n≥2)
所以,当n≥2时,
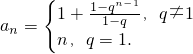
.
上式对n=1显然成立.故有
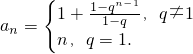
.
(3)q=1符合题意;
若q≠1,
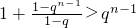
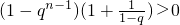
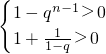
或
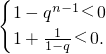
解得:q∈(0,1)∪(1,2).
综上,q∈(0,2)..
分析:(1)将已知递推关系变形,利用等比数列的定义,证得数列{b
n}是等比数列.
(2)先利用等比数列的通项公式求出b
n,再用叠加法求出数列{a
n}的通项公式.
(3)将两个数列的通项代入不等式得到关于d的不等式,将不等式因式分解,求出d的范围.
点评:本题考查证明一个数列是等比数列的方法是利用等比数列的定义;利用等比数列的前n项和的公式时,一定注意公比为1时要分类讨论.

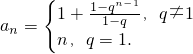 .
.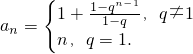 .
.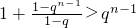
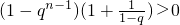
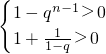 或
或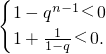


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案