
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知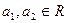 且
且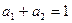 ,求证
,求证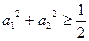
证明:构造 函数
函数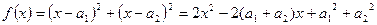 因为对一切
因为对一切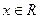 ,恒有
,恒有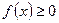 ,所以
,所以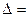 4-8
4-8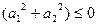 ,从而
,从而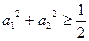
(1)若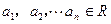 ,且
,且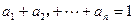 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若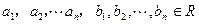 ,求证
,求证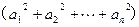
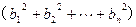
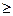
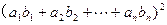 .[
.[
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:2010-2011年浙江省宁海县正学中学高二下学期第二次阶段性考试文数 题型:解答题
(本小题15分)
已知函数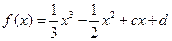 有极值.
有极值.
(1)求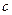 的取值范围;
的取值范围;
(2)若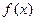 在
在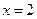 处取得极值,且当
处取得极值,且当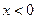 时,
时,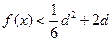 恒成立,求
恒成立,求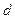 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省宁海县正学中学高二下学期第二次阶段性考试重点班文数 题型:解答题
(本小题15分)
如图在三棱锥P-ABC中,PA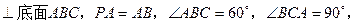
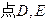 分别在棱
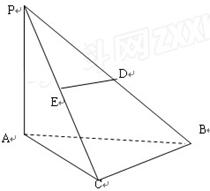
分别在棱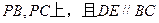 ,
,
(1)求证:BC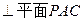
(2)当D为PB中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角,并说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期学段考试数学理卷 题型:解答题
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知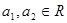 且
且 ,求证
,求证
证明:构造函数 因为对一切
因为对一切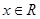 ,恒有
,恒有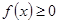 ,所以
,所以 4-8
4-8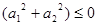 ,从而
,从而
(1)若 ,且
,且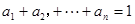 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若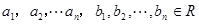 ,求证
,求证
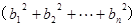
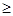
 .[
.[
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期学段考试数学理卷 题型:解答题
(本小题15分)
设 是虚数,
是虚数, 是实数,且
是实数,且 。
。
(1)求 的值及
的值及 的实部的取值范围;
的实部的取值范围;
(2)设 ,求证
,求证 为纯虚数;
为纯虚数;
(3)求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com