练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，已知a、b和锐角A，要使三角形有两解，则应满足的条件是（ ）
    A．a=bsinA
    B．bsinA＞a
    C．bsinA＜b＜a
    D．bsinA＜a＜b
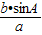
    【答案】分析：由正弦定理可得 sinB=，再由 sinB=＞sinA，且 sinB=＜1，可得a、b的关系，从而得到结论．
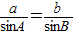
    解答：解：由正弦定理可得 ，∴sinB=．
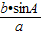
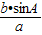
    由锐角A，要使三角形有两解，则 sinB=＞sinA，∴b＞a．
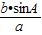
    再由 sinB=＜1 可得 bsinA＜a．
    综上可得 b＞a＞bsinA，
    故选：D．
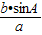
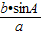
    点评：本题主要考查正弦定理的应用，判断sinB=＞sinA，且sinB=＜1，是解题的关键，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，已知A、B、C成等差数列，求tg（
    A
    2
    ）+
    		3
    tg（
    A
    2
    ）tg（
    C
    2
    ）+tg（
    C
    2
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知A=45°，a=2，b=
    		2
    ，则B等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知a=
    		3
    ，b=
    		2
    ，1+2cos（B+C）=0，求：
    （1）角A，B； 
    （2）求BC边上的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知A=60°，
    AB
    •
    AC
    =1，则△ABC的面积为
    		3
    2
    		3
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知a=1，b=2，cosC=
    34
    ．
    （1）求AB的长；
    （2）求sinA的值．

    查看答案和解析>>

    同步练习册答案