
【题目】【四川省高2017届第一次名校联考(广志联考)(理)】已知函数![]() .
.
(Ⅰ)当![]() 时,存在
时,存在![]() 使不等式
使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:
试题解析:(I)借助存在型不等式成立的条件建立不等式;(II)先建立不等式,再运用导数知识求解:
解:(Ⅰ)当![]() 时,
时,![]() ,
,
所以![]() ,由
,由![]() 知
知![]() ,
,
则函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则当![]() 时,
时,![]() ,
,
故存在![]() 使不等式
使不等式![]() 成立,
成立,
只需![]() 即可.
即可.
(Ⅱ)在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方等价于对任意
的下方等价于对任意![]() ,
,![]() ,
,
即![]() 恒成立,
恒成立,
设![]() ,
,![]() .
.
则![]()
当![]() 时,
时,![]() ,
,![]() .
.
①若![]() ,即
,即![]() ,有
,有![]() ,
,
则函数![]() 在区间
在区间![]() 为减函数,
为减函数,
则对任意![]() ,
,![]() ,
,
只需![]() ,即当
,即当![]() 时,
时,![]() 恒成立.
恒成立.
②若![]() ,即
,即![]() 时,
时,
令![]() ,
,
得![]() .
.
则函数![]() 在区间
在区间![]() 为减函数,在区间
为减函数,在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
③若![]() ,即当
,即当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
综上,当![]() 时,
时,![]() 在区间
在区间![]() 恒成立,
恒成立,
即当![]() 时,在区间
时,在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方.
的下方.


科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 的图象与x轴无交点,求a的取值范围;
的图象与x轴无交点,求a的取值范围;
(2) 若函数![]() 在[-1,1]上存在零点,求a的取值范围;
在[-1,1]上存在零点,求a的取值范围;
(3)设函数![]() ,当
,当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求b的取值范围.
,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数![]() 是增函数,命题Q:
是增函数,命题Q:![]()
(1)写出命题Q的否命题![]() ,并求出实数
,并求出实数![]() 的取值范围,使得命题
的取值范围,使得命题![]() 为真命题;
为真命题;
(2)如果![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]()
的中点,AC⊥平面BCC1B1.
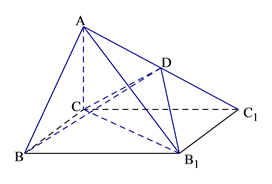
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求三棱锥C-DB1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。

(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(3)若高二年级这次竞赛的合格率为![]() ,由以上统计数据填写下面
,由以上统计数据填写下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
 附:参考数据与公式
附:参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3ax2+2bx+c,a+b+c=0,f(0)>0,f(1)>0,证明a>0,并利用二分法证明方程f(x)=0在区间[0,1]内有两个实根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com