
【题目】一个简单图中两两相邻的t个项点称为一个团,与其余每个顶点均相邻的顶点称为中心点.给定整数![]() 及满足
及满足![]() 的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为
的整数k,一个n阶简单图G中不存在k+1团,其全部k团记为![]() .
.
(1)证明:![]() ;
;
(2)若在图G中再添加一条边就存在k+1团,求图G的中心点个数的最小值.
【答案】(1)见解析;(2)见解析
【解析】
将题给方程两边模3得![]() .从而,
.从而,![]() .
.
记![]() .
.
1.当y=1时,原方程为![]() .
.
上式两边模13得![]() .
.
从而,![]() .记
.记![]() .
.
则原方程化为![]() ①
①
式①两边模5得![]() .
.
从而,![]()
则式①两边模16得![]() ,矛盾.
,矛盾.
2.当![]() 时,原方程两边模8得
时,原方程两边模8得![]() .
.
从而,![]() .记
.记![]() .
.
则原方程化为![]() .
.
![]() .
.
注意到,![]() .
.
故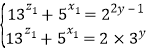 ②
②
或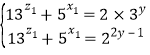 ③
③
由方程组②得![]() ④
④
式④两边模4得![]() .
.
从而,y为奇数.
则式④两边模5得![]() ,矛盾.
,矛盾.
故方程组②无解.
由方程组③得![]()
上式两边模4得![]() .
.
从而,y为偶数.
记![]() ,则原方程化为
,则原方程化为![]()
![]() .
.
注意到,![]() .
.
则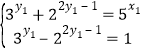 .
.
若![]() ,由
,由![]() ,等式两边模4得
,等式两边模4得![]() .
.
从而,![]() .
.
记![]() ,则原方程化为
,则原方程化为![]() .
.
注意到,![]() .
.
则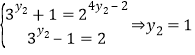 .
.
但此时![]() ,
,![]() ,矛盾.
,矛盾.
故![]() ,
,![]() ,
,![]() .
.
即![]() .
.
四、1.记![]() .
.
即证![]() ①
①
当m=1时,![]() .
.
假设式①对![]() 成立.
成立.
对m,记![]() ,
,![]() ,
,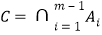 ,
,![]() .
.
则![]() ,
,![]() ,
,![]() .
.
故![]()
![]() ②
②
下面证明:![]()
因为集合C中每个点与集合A中所有点相邻,所以,![]() 组成团,但不是k+1团.
组成团,但不是k+1团.
故![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
则![]() .
.
于是,由式②得![]()
故式①对正整数m也成立.
由数学归纳法,不等式得证.
2.本题条件中“差一条边就含k+1团”,属于“极图”特征.此时,有![]() .
.
事实上,假设![]() .则存在图G的某个顶点
.则存在图G的某个顶点![]() ,从而,顶点v必与集合
,从而,顶点v必与集合![]() 中某个顶点u不相邻.否则,
中某个顶点u不相邻.否则,![]() 构成k+1团,与极图G矛盾.现添上一条边vu,由题设条件,知图G存在k+1团,记作
构成k+1团,与极图G矛盾.现添上一条边vu,由题设条件,知图G存在k+1团,记作![]() ,则
,则![]() 是图G的一个k团,亦矛盾.
是图G的一个k团,亦矛盾.
记图G中全部中心点的集合为C.则![]() .
.
再由1得![]() .
.
构造等号成立的例子.令![]() .
.
其中,除点![]() 与
与![]() 不相邻外,其他任意两点均相邻.则该图G的中心点的集合为
不相邻外,其他任意两点均相邻.则该图G的中心点的集合为![]() ,并且不存在k+1团(因为任取图G的k+1个顶点,总包含一点对
,并且不存在k+1团(因为任取图G的k+1个顶点,总包含一点对![]() 、
、![]() ,但任意添加一条边
,但任意添加一条边![]()
![]() ,总能出现k+1团
,总能出现k+1团![]() ,G是极图.
,G是极图.
故图G中心点个数![]() .
.
综上,图G中心点个数的最小值为![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】对一堆100粒的石子进行如下操作:每次任选石子数大于1的一堆任意分成不空的两堆,直到每堆1粒(100堆)为止.证明:
(1)无论如何操作,必有某个时刻存在20堆,其石子总数为60;
(2)可以进行适当地操作使得任何时刻不存在19堆,其石子总数为60.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A.264B.72C.266D.274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次不等式ax2+x+b>0的解集为(-∞,-2)∪(1,+∞).
(Ⅰ)求a和b的值;
(Ⅱ)求不等式ax2-(c+b)x+bc<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国人民大学发布的《中国大学生创业报告》显示,在国家“双创”政策的引导下,随着社会各方对于大学生创业实践的支持力度不断加强,大学生创业意向高涨,近九成的在校大学生曾考虑过创业,近两成的学生有强烈的创业意向. 数据充分表明,大学生正以饱满的热情投身到创新创业的大潮之中,大学生创业实践正呈现出生机勃勃的态势。小张大学毕业后从2008年年初开始创业,下表是2019年春节他将自己从2008—2018年的净利润按年度给出的一个总的统计表(为方便运算,数据作了适当的处理,单位:万元).
年度 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
利润 | 6 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 |
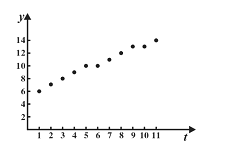
(Ⅰ)散点图如图所示,根据散点图指出年利润![]() (单位:万元)和年份序号
(单位:万元)和年份序号![]() 之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润
之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间关系的效果;
之间关系的效果;
(Ⅱ)试用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间的关系:求出年净利润
之间的关系:求出年净利润![]() 关于年份序号
关于年份序号![]() 的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
附注:参考数据![]() .
.
参考公式: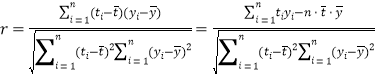 .
.![]() 且
且![]() 越大拟合效果越好.回归方程
越大拟合效果越好.回归方程![]() 斜率的最小二乘法估计公式为:
斜率的最小二乘法估计公式为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司在2020年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利40%,也可能亏损10%,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备据市场调研,投资到该项目上,到年底可能获利50%,可能损失30%,也可能不赔不赚,且这三种情况发生的概率分别为![]() ,
,![]() 和
和![]() .针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
.针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
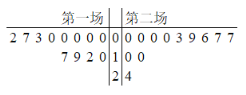
A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: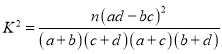 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com