分析:(I)根据题意,可证出四边形BCEF是平行四边形,得BE∥CF,结合线面平行判定定理即可证出BE∥平面ACF;
(II)过D作DH∥AE交AD于H,由AD⊥平面AEB得AD⊥AE,结合AE⊥AB证出AE⊥平面ABCD,可得FH⊥平面ABCD,从而得到FH⊥AC.再由题中条件证出四边形ABCH为正方形,得BH⊥AC,从而证出AC⊥平面BFH,可得BF⊥AC;
(III)作HG⊥DF于G,连结CG,由前面的证明可得CH⊥平面AEFD,由三垂线定理结合HG⊥DF得到CG⊥DF,可得∠CGH是二面角C-DF-E的平面角.然后在Rt△CHG中,分别算出HG、CG之长,得到cos∠CGH=
=
,即得二面角C-DF-E的余弦值.
解答:解:(Ⅰ)∵AD∥EF,AD∥BC,∴EF∥BC.
又∵BC=EF=2,∴四边形BCEF是平行四边形,可得BE∥CF.
∵BE?平面ACF,CF?平面ACF,∴BE∥平面ACF;
(Ⅱ)∵AD⊥平面AEB,AE?平面AEB,∴AD⊥AE,
又∵AE⊥AB,AD∩AD=A,AB、AD?平面ABCD,
∴AE⊥平面ABCD.
平面AEFD内,过D作DH∥AE交AD于H,则FH⊥平面ABCD.
∵AC?平面ABCD,∴FH⊥AC.
连结CH、BH,则
∵平行四边形AEFH中,AH=EF=2
∴BC∥AH,BC=AH=2,可得四边形ABCH平行四边形,
∵AB=BC=2,∴四边形ABCH为正方形,可得BH⊥AC
又BH∩FH=H,BH?平面BFH,FH?平面BFH,
∴AC⊥平面BFH,结合BD?平面BHD,可得BF⊥AC;
(III)作HG⊥DF于G,连结CG
∵AE⊥平面ABCD,AE?平面AEFD,∴平面ABCD⊥平面AEFD
∵CH⊥AD,平面ABCD∩平面AEFD=AD,CH?平面ABCD
∴CH⊥平面AEFD,可得HG是CG在平面AEFD的射影
∵HG⊥DF,∴CG⊥DF,可得∠CGH是二面角C-DF-E的平面角
∵Rt△DFH中,FH=2,DH=AD-AH=1,
∴DF=
=
,可得HG=
=
因此,Rt△CHG中,CG=
=
∴cos∠CGH=
=
,即二面角C-DF-E的余弦值为
.

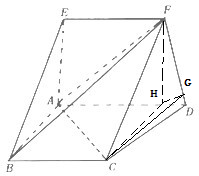
 (2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3
(2013•泰安二模)在如图的多面体中,AD⊥平面ABE,AE⊥AB,EF∥AD,AD∥BC,AE=AB=BC=EF=2,AD=3


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案