
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
【答案】
(1)解:∵直线l1的参数方程为 ![]() ,(t为参数),
,(t为参数),
∴消掉参数t得:直线l1的普通方程为:y=k(x﹣2)①;
又直线l2的参数方程为 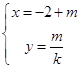 ,(m为参数),
,(m为参数),
同理可得,直线l2的普通方程为:x=﹣2+ky②;
联立①②,消去k得:x2﹣y2=4,即C的普通方程为x2﹣y2=4(x≠±2)
(2)解:∵l3的极坐标方程为ρ(cosθ+sinθ)﹣ ![]() =0,
=0,
∴其普通方程为:x+y﹣ ![]() =0,
=0,
联立 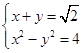 得:
得: 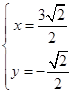 ,
,
∴ρ2=x2+y2= ![]() +
+ ![]() =5.
=5.
∴l3与C的交点M的极径为ρ= ![]()
【解析】解:(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x﹣2)①与x=﹣2+ky②;联立①②,消去k可得C的普通方程为x2﹣y2=4;(2)将l3的极坐标方程为ρ(cosθ+sinθ)﹣ ![]() =0化为普通方程:x+y﹣
=0化为普通方程:x+y﹣ ![]() =0,再与曲线C的方程联立,可得
=0,再与曲线C的方程联立,可得 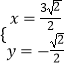 ,即可求得l3与C的交点M的极径为ρ=
,即可求得l3与C的交点M的极径为ρ= ![]() .
.


科目:高中数学 来源: 题型:
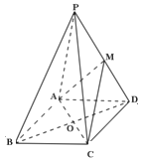
【题目】如图,已知在正四棱锥![]() 中,
中, ![]() 为侧棱
为侧棱![]() 的中点, 连接
的中点, 连接![]() 相交于点
相交于点![]() 。
。
(1)证明: ![]() ;
;
(2)证明: ![]() ;
;
(3)设![]() ,若质点从点
,若质点从点![]() 沿平面
沿平面![]() 与平面
与平面![]() 的表 面运动到点
的表 面运动到点![]() 的最短路径恰好经过点
的最短路径恰好经过点![]() ,求正四棱锥
,求正四棱锥 ![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]()
![]() ,使得函数
,使得函数![]() 同时满足:
同时满足:
(1)![]() 在
在![]() 内是单调函数;
内是单调函数;
(2)![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的“
的“![]() 倍值区间”.
倍值区间”.
下列函数中存在“3倍值区间”的有_____.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,一个焦点F(﹣2,0),且长轴长与短轴长的比是 ![]() .
.
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当 ![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 上的点
上的点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,记
,记![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)设过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,试问:是否存在直线
两点,试问:是否存在直线![]() ,使以
,使以![]() 为直径的圆经过原点?若存在,求出直线
为直径的圆经过原点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
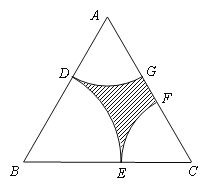
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD的所有棱长均为6,点P在AC上,且AP=2PC,过P作四面体的截面,使截面平行于直线AB和CD,则该截面的周长为( )
A.16
B.12
C.10
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com