
设函数 .
.
(1)
求 的单调区间与极值;
的单调区间与极值;
(2)是否存在实数 ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
(1) 的单调递减区间是
的单调递减区间是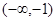 ,单调递增区间是
,单调递增区间是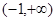 .
.  极小值=
极小值=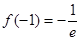 (2)
(2) 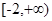 .
.
【解析】
试题分析:(1)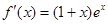 .令
.令 ,得
,得 ;
1分
;
1分
列表如下
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
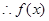 的单调递减区间是
的单调递减区间是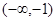 ,单调递增区间是
,单调递增区间是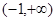 .
4分
.
4分
 极小值=
极小值=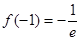 5分
5分
(2) 设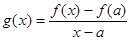 ,由题意,对任意的
,由题意,对任意的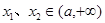 ,当
,当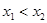 时恒有
时恒有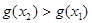 ,即
,即 在
在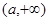 上是单调增函数.
7分
上是单调增函数.
7分
 8分
8分
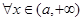 ,
,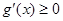
令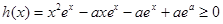

 10分
10分
若 ,当
,当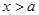 时,
时,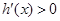 ,
,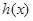 为
为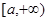 上的单调递增函数,
上的单调递增函数,
 ,不等式成立.
11分
,不等式成立.
11分
若 ,当
,当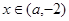 时,
时,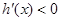 ,
,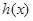 为
为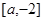 上的单调递减函数,
上的单调递减函数,
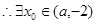 ,
,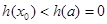 ,与
,与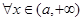 ,
, 矛盾
12分
矛盾
12分
所以,a的取值范围为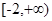 .
13分
.
13分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2012-2013学年辽宁省本溪一中高三(上)第二次月考数学试卷(文科)(解析版) 题型:解答题
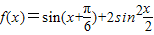 .
. ,求b值.
,求b值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省永州市蓝山二中高三第四次联考数学试卷(文科)(解析版) 题型:解答题
 .
. ,求a的值.
,求a的值.查看答案和解析>>
科目:高中数学 来源:2010年上海市长宁区高考数学一模试卷(理科)(解析版) 题型:解答题
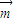 =(
=(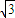 sin2x-1,cosx),
sin2x-1,cosx),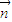 =(1,2cosx),设函数
=(1,2cosx),设函数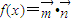 .
.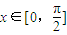 时的最大值;
时的最大值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com