
【题目】已知函数![]() ,
,![]() .
.
(1)若直线![]() 是曲线
是曲线![]() 的一条切线,求k的值;
的一条切线,求k的值;
(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 无交点,求整数k的最大值.
无交点,求整数k的最大值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F的直线交抛物线C于
的焦点为F,过F的直线交抛物线C于![]() ,
,![]() 两点.
两点.
(Ⅰ)当![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)过点A作抛物线准线的垂线,垂足为E,过点B作EF的垂线,交抛物线于另一点D,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王于2015年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还贷方式,且截止2019年底,他没有再购买第二套房子.下图是2016年和2019年小王的家庭收入用于各项支出的比例分配图,根据以上信息,判断下列结论中正确的是( )
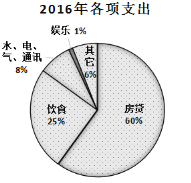
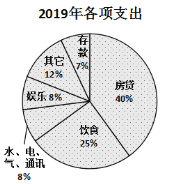
A.小王一家2019年用于饮食的支出费用跟2016年相同
B.小王一家2019年用于其他方面的支出费用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了1倍
D.小王一家2019年用于房贷的支出费用比2016年减少了
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点的极坐标;
的交点的极坐标;
(2)设![]() 是
是![]() 的一条直径,且
的一条直径,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 交
交![]() 于
于![]() 两点,直线
两点,直线![]() 交
交![]() 于
于![]() 两点,求四边形
两点,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动被誉为“世界第一运动”.为推广足球运动,某学校成立了足球社团由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如下:
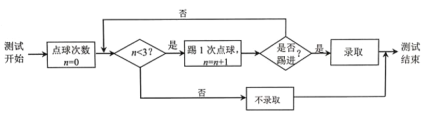
(1)下表是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为![]() ,求
,求![]() ;
;
![]()
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,接到第n次传球的人即为第![]() 次触球者
次触球者![]() ,第n次触球者是甲的概率记为
,第n次触球者是甲的概率记为![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接写出结果即可);
(直接写出结果即可);
(ii)证明:数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 经过
经过![]() ,且右焦点坐标为
,且右焦点坐标为![]() .
.
(1)求椭圆的标准方程;
(2)设A,B为椭圆的左,右顶点,C为椭圆的上顶点,P为椭圆上任意一点(异于A,B两点),直线AC与直线BP相交于点M,直线BC与直线AP相交于点N,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 上一点,以点
上一点,以点![]() 及椭圆的左、右焦点
及椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形面积为
为顶点的三角形面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作斜率存在且互相垂直的直线
作斜率存在且互相垂直的直线![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 两交点的中点,
两交点的中点,![]() 是
是![]() 与
与![]() 两交点的中点,求△
两交点的中点,求△![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c均为正数,设函数f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函数f(x)的最大值为1,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com