
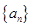 的首项为
的首项为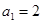 ,公比为
,公比为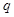 (
(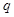 为正整数),且满足
为正整数),且满足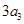 是
是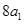 与
与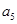 的等差中项;数列
的等差中项;数列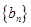 满足
满足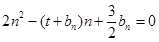 (
(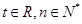 ).
).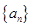 的通项公式;
的通项公式;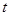 的值,使得数列
的值,使得数列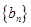 为等差数列;
为等差数列;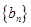 为等差数列时,对每个正整数
为等差数列时,对每个正整数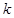 ,在
,在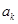 与
与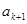 之间插入
之间插入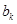 个2,得到一个新数列
个2,得到一个新数列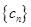 . 设
. 设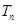 是数列
是数列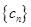 的前
的前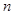 项和,试求满足
项和,试求满足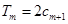 的所有正整数
的所有正整数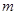 .
.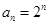 ;(Ⅱ)
;(Ⅱ)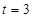 时,数列
时,数列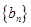 为等差数列;(Ⅲ)
为等差数列;(Ⅲ)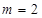
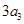 是
是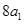 与
与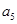 的等差中项,由等差中项不难得出三者的关系
的等差中项,由等差中项不难得出三者的关系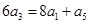 ,又由
,又由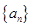 为等比数列,回归基本量即可求出公比
为等比数列,回归基本量即可求出公比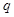 的值,就可求出的通项公式; (Ⅱ)由数列
的值,就可求出的通项公式; (Ⅱ)由数列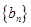 满足
满足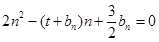 ,可化简求得
,可化简求得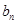 的表达式,即
的表达式,即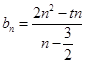 ,由(Ⅱ)中所给条件
,由(Ⅱ)中所给条件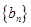 为等差数列,可想到它的前三项一定符合等差数列的要求,即满足
为等差数列,可想到它的前三项一定符合等差数列的要求,即满足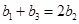 ,可求出
,可求出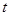 的值,这样得到
的值,这样得到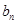 的表达式,通过等差数列的定义对所求
的表达式,通过等差数列的定义对所求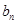 表达式进行验证,得出是一个等差数列;(Ⅲ)由题目在
表达式进行验证,得出是一个等差数列;(Ⅲ)由题目在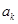 与
与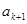 之间插入
之间插入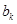 个2,即
个2,即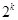 和
和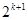 之间插入2k个2,这样不难发现这个数列的前三项均为2,这
之间插入2k个2,这样不难发现这个数列的前三项均为2,这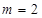 显然成立,推到一般情形去证明当
显然成立,推到一般情形去证明当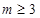 时,等式左边
时,等式左边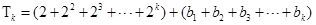 ,右边
,右边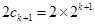 ,化简得
,化简得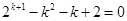 ,可根据特点可令函数
,可根据特点可令函数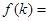
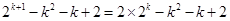 ,可对其求导进行分析函数的单调性情况,发现最小值
,可对其求导进行分析函数的单调性情况,发现最小值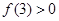 成立,从而就可得出符合题意的
成立,从而就可得出符合题意的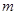 值.
值.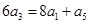 ,所以
,所以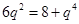 ,
,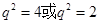 (舍),则
(舍),则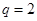 3分
3分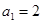 ,所以
,所以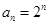 5分
5分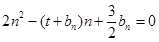 ,得
,得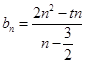 ,
,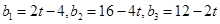 ,
,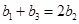 ,得
,得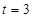 8分
8分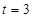 时,
时,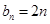 ,由
,由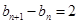 (常数)知此时数列
(常数)知此时数列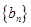 为等差数列 10分
为等差数列 10分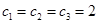 ,易知
,易知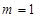 不合题意,
不合题意,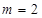 适合题意 11分
适合题意 11分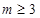 时,若后添入的数2
时,若后添入的数2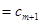 ,则一定不适合题意,从而
,则一定不适合题意,从而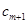 必是数列
必是数列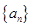 中的
中的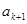 ,则
,则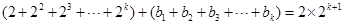 ,
,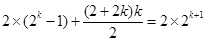 ,即
,即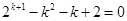 13分
13分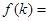
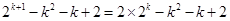 ,则
,则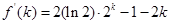 ,
,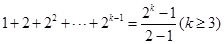 ,
,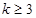 时,
时,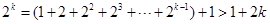 ,又
,又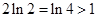 ,
,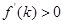 ,故
,故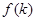 在[3,
在[3,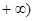 递增.
递增.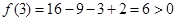 知
知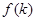 =0在[3,
=0在[3,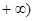 无解,
无解,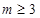 都不合题意 15分
都不合题意 15分

科目:高中数学 来源:不详 题型:解答题
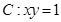 ,过
,过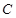 上一点
上一点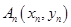 作一斜率为
作一斜率为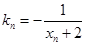 的直线交曲线
的直线交曲线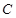 于另一点
于另一点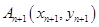 (
(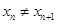 且
且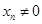 ,点列
,点列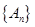 的横坐标构成数列
的横坐标构成数列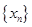 ,其中
,其中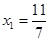 .
.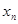 与
与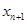 的关系式;
的关系式;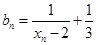 ,求证:数列
,求证:数列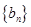 是等比数列;
是等比数列;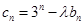 (
(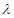 为非零整数,
为非零整数,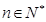 ),试确定
),试确定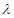 的值,使得对任意
的值,使得对任意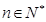 ,都有
,都有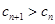 成立.
成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com