
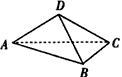
| 解:(1)如图,设F为AC的中点,由于AD=CD, 所以DF⊥AC 故由平面ABC⊥平面ACD,知DF⊥平面ABC, 即DF是四面体ABCD的面ABC上的高,且DF=ADsin30°=1,AF=ADcos30°= 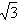 在Rt△ABC中,因AC=2AF=2 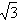 ,AB=2BC, ,AB=2BC,由勾股定理易知 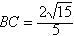 , ,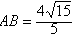 故四面体ABCD的体积 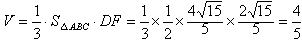 。 。(2)如图,设G,H分别为CD,BD的中点,则FG ∥AD,GH∥BC 从而∠FGH是异面直线AD与BC所成的角或其补角, 设E为边AB的中点,则EF∥BC, 由AB⊥BC,知EF⊥AB 又由(1)有DF⊥平面ABC, 故由三垂线定理知DE⊥AB 所以∠DEF为二面角C-AB-D的平面角 由题设知∠DEF=60°, 设AD=a,则DF=AD·sin∠CAD= 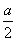 在Rt△DEF中,EF=DF·cot∠DEF= 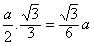 从而 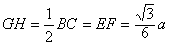 因Rt△ADF≌Rt△BDF,故BD=AD=a, 从而,在Rt△BDF中, 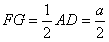 又 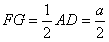 , ,从而在△FGH中,因FG=FH,由余弦定理得 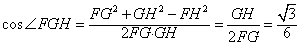 因此,异面直线AD与BC所成角的余弦值为 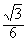 。 。 |
 |


科目:高中数学 来源: 题型:
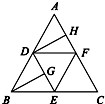 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为查看答案和解析>>
科目:高中数学 来源: 题型:
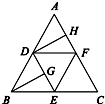 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )查看答案和解析>>
科目:高中数学 来源: 题型:
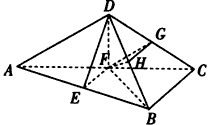
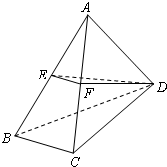 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
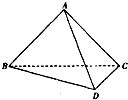 (2009•武汉模拟)如图,在四面体A-BCD中,AB=AD=
(2009•武汉模拟)如图,在四面体A-BCD中,AB=AD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
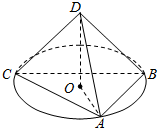 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com