
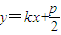 交于A、B两点,O为坐标原点.
交于A、B两点,O为坐标原点.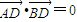 ?如果存在,求出点D的坐标;如不存在,说明理由.
?如果存在,求出点D的坐标;如不存在,说明理由.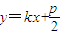 联立.
联立.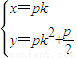 ,消去k,可得点C的轨迹方程.
,消去k,可得点C的轨迹方程. 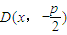 ,使
,使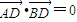 ,结合x1+x2=2pk,x1x2=-p2,y1+y2=2pk2+p,
,结合x1+x2=2pk,x1x2=-p2,y1+y2=2pk2+p,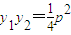 ,可知对于任意实数k,在l上存在点
,可知对于任意实数k,在l上存在点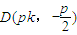 ,使得
,使得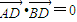 .
.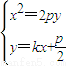 ,∴x2-2pkx-p2=0,∴x1+x2=2pk,x1x2=-p2,∴y1+y2=2pk2+p,
,∴x2-2pkx-p2=0,∴x1+x2=2pk,x1x2=-p2,∴y1+y2=2pk2+p,
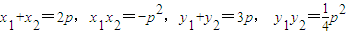 ,∴AB=4p
,∴AB=4p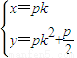 ,消去k,得
,消去k,得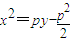 .
.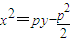 .
. 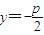
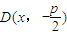 ,使
,使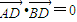 ,则有
,则有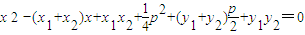 ①
①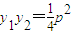 ,代入①式,整理得(x-pk)2=0,∴x=pk.
,代入①式,整理得(x-pk)2=0,∴x=pk.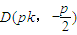 ,使得
,使得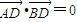 .
.

科目:高中数学 来源: 题型:
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2| p |
| p |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:黑龙江省大庆实验中学2010-2011学年高二上学期期末考试数学理科试题 题型:013
已知抛物线x2=2py(p>0),过点![]() 向抛物线引两条切线,A、B为切点,则线段AB的长度是
向抛物线引两条切线,A、B为切点,则线段AB的长度是
2p
p
![]()
![]()
查看答案和解析>>
科目:高中数学 来源:广东省广州市2007年高三年级六校联考数学理科试卷 题型:044
已知抛物线x2=2py(p>0),过动点M(0,a),且斜率为1的直线L与该抛物线交于不同两点A、B,|AB|≤2p,
(1)求a的取值范围;
(2)若p=2,a=3,求直线L与抛物线所围成的区域的面积;
查看答案和解析>>
科目:高中数学 来源:2010年江西省名校高考信息卷一(理) 题型:选择题
已知抛物线x2 = 2py (p > 0),过点M (0 , - )向抛物线引两条切线,A、B为切点,则线段
AB的长度是
|
A.2p |
B.p |
C. |
D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com