练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年南昌市一模理）（12分）已知F1、F2是椭圆的两个焦点，O为坐标原点，点P）在椭圆上，线段PF2与y轴的交点M满足；⊙O是以F1F2为直径的圆，一直线l: y=kx+m与⊙O相切，并与椭圆交于不同的两点A、B.

     （1）求椭圆的标准方程；

     （2）当，且满足时，求△AOB面积S的取值范围.

    解析：（1）∴点M是线段PF2的中点 

    ∴OM是△PF1F2的中位线 ,

    又OM⊥F1F2  ∴PF1⊥F1F2

       

    ∴椭圆的标准方程为=1………………5分

       （2）∵圆O与直线l相切 

            由

        ∵直线l与椭圆交于两个不同点，,  设，则

           

       

         

          …………………………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年南昌市一模理）( 14分) 已知数列满足

    （1）  求数列的通项公式；

    （2）  设b= (n∈N,n≥2), b,

    ①求证：b+b+……+b< 3 ;

    ②设点M(n,b)((n∈N,n>2)在这些点中是否存在两个不同的点同时在函数

    y =(k>0)的图象上,如果存在,求出点的坐标,若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年南昌市一模理）（12分）已知函数f (x) =lnx,g(x) =，（a为常数），若直线l与y =f(x), y =g(x)的图象都相切，且l与y = f(x)的图象相切的切点的横坐标为1.

    （1）求直线l的方程及a的值；

    （2） 当 2 ≤m <时,求h(x)= f(x)―f(x)[2g(x)- m +1]在[,2]上的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

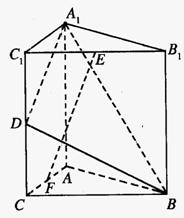
    （08年南昌市一模理）（12分）如图，直三棱柱A1B1C1―ABC中，C1C=CB=CA=2，AC⊥CB. D、E分别为棱C1C、B1C1的中点.

    （1）求与平面A1C1CA所成角的大小；

    （2）求二面角B―A1D―A的大小；

    （3）在线段AC上是否存在一点F，使得EF⊥平面A1BD？若存在，确定其位置并证明结论；若不存在，说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年南昌市一模理） 正三棱锥S―ABC中，M是SC的中点，=0，若侧棱，则此正三棱锥S―ABC外接球的表面积是

    A．36π      B．64π         C．144π        D．256π

    查看答案和解析>>

    同步练习册答案