
分析 利用命题的否定判断①的正误;函数的奇偶性判断②的正误;方程的解判断③的正误;三角形中碳钢正弦定理判断④的正误;
解答 解:对于①?x∈(0,2),3x>x3的否定是:?x∈(0,2),3x≤x3;满足命题的否定形式,正确;
②若f(x)=2x-2-x,则?x∈R,f(-x)=2-x-2x=-(2x-2-x)=-f(x);函数是奇函数,正确;
③若f(x)=x+$\frac{1}{x+1}$,x+$\frac{1}{x+1}$=1,可得x2+x+1=x+1,解得x=0,所以?x0∈(0,+∞),f(x0)=1;不正确;
④在△ABC中,若A>B,则sin A>sin B.在三角形中大角对大边,∵A>B,∴a>b,由正弦定理可得
从而a=2RsinA,b=2RsinB,∴2RsinA>2RsinB,∴sinA>sinB.所以④正确.
故答案为:①②④.
点评 本题考查命题的真假的判断与应用,考查命题的否定函数的奇偶性,解三角形,是基本知识的考查.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
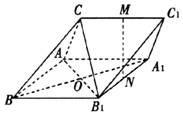 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com