
【题目】已知数列{an},a1=2,a2=6,且满足![]() =2(n≥2且n∈N+)
=2(n≥2且n∈N+)
(1)证明:新数列{an+1-an}是等差数列,并求出an的通项公式
(2)令bn=![]() ,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
,设数列{bn}的前n项和为Sn,证明:S2n-Sn<5
【答案】(1)见解析.(2)见解析.
【解析】试题分析:(1)由已知可得![]() ,则
,则![]() ,即可证明
,即可证明![]() 是等差数列,进而求出
是等差数列,进而求出![]() 的通项公式;
的通项公式;
试题解析:(1)证明:an+1+an-1=2an+2,则(an+1-an)-(an-an-1)=2.所以{an+1-an}是公差为2的等差数列.
n≥2,an=(an-an-1)+…+(a2-a1)+a1=2n+…+4+2=2·![]() =n(n+1).
=n(n+1).
当n=1,a1=2满足. 则an=n(n+1).
(2)bn=![]() -
-![]() =
=![]() -
-![]() ∴Sn=10(1+
∴Sn=10(1+![]() +…+
+…+![]() )-
)-![]() ,
,
∴S2n=10(1+![]() +…+
+…+![]() +
+![]() )-
)-![]() ,
,
设Mn=S2n-Sn=10(![]() )-
)-![]() ,
,
∴Mn+1=10(![]() )-
)-![]() ,
,
∴Mn+1-Mn=10(![]() )-
)-![]() =10(
=10(![]() ) -
) -![]() =
=![]() -
-![]() ,
,
∴当n=1时, Mn+1-Mn=![]() >0,即M1<M2,当n≥2时,Mn+1-Mn<0,
>0,即M1<M2,当n≥2时,Mn+1-Mn<0,
即M2>M3>M4>…,∴(Mn)max=M2=10×(![]() )-1=
)-1=![]()
则S2n-Sn≤S4-S2=![]()


科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4 及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn} 的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC上的射影D为BC的中点,则异面直线AB与CC1所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥P﹣ABCD中,AB=2,PA= ![]() ,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点. 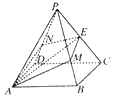
(1)若PM= ![]() PB,PN=λPD,求λ的值;
PB,PN=λPD,求λ的值;
(2)求直线PA与平面AMEN所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD= ![]() ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点.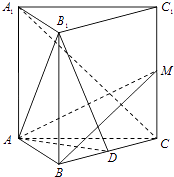
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都是正数,且对任意n∈N*都有a13+a23+a33+…+an3=Sn2 , 其中Sn为数列{an}的前n和.
(1)求证:an2=2Sn﹣an;
(2)求数列{an}的通项公式
(3)设bn=3n+(﹣1)n﹣1λ2 ![]() (λ为非零整数,n∈N*)试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.
(λ为非零整数,n∈N*)试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() AD与BC交于点M,设
AD与BC交于点M,设![]() ,以
,以![]() 、
、![]() 为基底表示
为基底表示![]()

【答案】![]()
【解析】试题分析:由A、M、D三点共线,知![]() ;由C、M、B三点共线,知
;由C、M、B三点共线,知![]()
,所以 ,所以
,所以![]() =
=![]() .
.
试题解析:
设![]() ,
,
则![]()
因为A、M、D三点共线,所以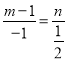 ,即
,即![]()
又![]()
因为C、M、B三点共线,所以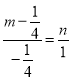 ,即
,即![]()
由![]() 解得
解得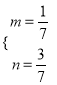 ,所以
,所以![]()
【题型】解答题
【结束】
20
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com