【题目】在合作学习小组的一次活动中，甲、乙、丙、丁、戊五位同学被随机地分配承担
，
，
，
四项不同的任务，每个同学只能承担一项任务.
（1）若每项任务至少安排一位同学承担，求甲、乙两人不同时承担同一项任务的概率；
（2）设这五位同学中承担任务的人数为随机变量
，求的分布列及数学期望
.
快捷英语周周练系列答案科目：高中数学 来源： 题型：
【题目】菜市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况，首先随机抽样其中200名购房者，并对其购房面积
（单位：平方米，
）进行了一次调查统计，制成了如图1所示的频率分布南方匿，接着调查了该市2018年1月﹣2019年1月期间当月在售二手房均价
（单位：万元/平方米），制成了如图2所示的散点图（图中月份代码1﹣13分别对应2018年1月至2019年1月）．
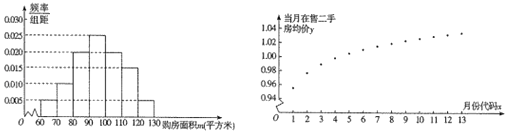
（1）试估计该市市民的平均购房面积
．
（2）现采用分层抽样的方法从购房耐积位于
的40位市民中随机取4人，再从这4人中随机抽取2人，求这2人的购房面积恰好有一人在
的概率．
（3）根据散点图选择
和
两个模型进行拟合，经过数据处理得到两个回归方程，分别为
和
，并得到一些统计量的值，如表所示：
|
| |
|
|
|
|
| |
请利用相关指数
判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年6月份的二手房购房均价（精确到
参考数据：
，
，
，
，
,
,
,
．参考公式：相关指数
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，椭圆C：
(a＞b＞0)经过点(0，
)，点F是椭圆的右焦点，点F到左顶点的距离和到右准线的距离相等．过点F的直线
交椭圆于M，N两点．
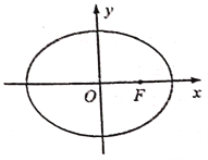
（1）求椭圆C的标准方程；
（2）当MF＝2FN时，求直线的方程；
（3）若直线上存在点P满足PM·PN＝PF2，且点P在椭圆外，证明：点P在定直线上．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题中正确命题的个数是（ ）
①对于命题
，使得
，则
，均有
；
②命题“已知x，
，若
，则
或
”是真命题；
③设
，
是非零向量，则“
”是“
”的必要不充分条件；
④
是直线
与直线
互相垂直的充要条件.
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某隧道的剖面图是由半圆及矩形
组成，交通部门拟在隧道顶部安装通风设备（视作点
），为了固定该设备，计划除从隧道最高点
处使用钢管垂直向下吊装以外，再在两侧自
两点分别使用钢管支撑.已知道路宽
，设备要求安装在半圆内部，所使用的钢管总长度为
.
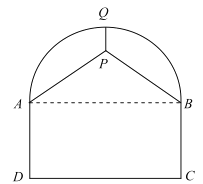
（1）①设
，将表示为关于
的函数；
②设
，将表示为关于
的函数；
（2）请选用（1）中的一个函数关系式，说明如何设计，所用的钢管材料最省？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设A，B分别为双曲线
(a>0，b>0)的左、右顶点，双曲线的实轴长为4
，焦点到渐近线的距离为.
(1)求双曲线的方程；
(2)已知直线y＝
x－2与双曲线的右支交于M，N两点，且在双曲线的右支上存在点D，使
，求t的值及点D的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，数轴
，
的交点为
，夹角为
，与轴、轴正向同向的单位向量分别是
，
.由平面向量基本定理，对于平面内的任一向量
，存在唯一的有序实数对
，使得
，我们把叫做点
在斜坐标系
中的坐标（以下各点的坐标都指在斜坐标系中的坐标）.
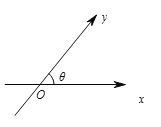
（1）若
，为单位向量，且与的夹角为
，求点的坐标；
（2）若
，点的坐标为
，求向量与的夹角；
（3）若
，求过点
的直线
的方程，使得原点到直线的距离最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
