
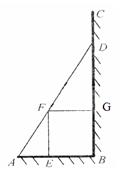
(本题13分)如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值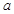 ,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积
,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积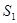 与种花的面积
与种花的面积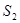 的比值
的比值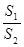 称为“草花比y”。
称为“草花比y”。
(1)设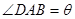 ,将
,将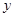 表示成
表示成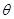 的函数关系式;
的函数关系式;
(2)当BE为多长时,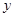 有最小值?最小值是多少?
有最小值?最小值是多少?
科目:高中数学 来源:2014届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分13分)如图,在平行六面体 中,
中,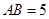 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.

(1)用 表示
表示 ;
;
(2)求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(一级学校) 题型:解答题
(本题满分13分)
如图,在五面体ABCDEF中,FA 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD,AF=AB=BC=FE=
AD,AF=AB=BC=FE= AD.
AD.
(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三5月月考调理科数学 题型:解答题
(本题满分13分)
如图,在三棱柱 中,已知
中,已知
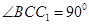 ,
,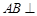 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;

(2)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若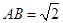 ,求二面角
,求二面角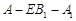 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题13分)如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
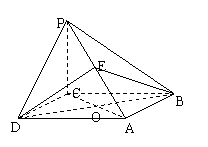 (1)求BE 与 CD所成的角.;
(1)求BE 与 CD所成的角.;
(2)求二面角![]() 的正切值。
的正切值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com