Question

【题目】如图，在菱形中，⊥平面，且四边形是平行四边形．

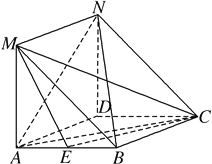
（1）求证：；

（2）当点在的什么位置时，使得∥平面，并加以证明．

Answer 1

【答案】(1）证明见解析；(2) 为的中点时，有平面，证明见解析.

【解析】试题分析：(1）连接，则，由线面垂直的性质可得，由线面垂直的判定定理可得平面，从而可得结论；(2)当为的中点时，设与交于，连接，由中位线定理可得,进而根据线面平行的判定定理可得结论.

试题解析：(1)证明：连接BD，则AC⊥BD.

由已知得DN⊥平面ABCD，因为AC平面ABCD，所以DN⊥AC.

因为DN平面NDB，BD平面NDB，DN∩DB＝D，

所以AC⊥平面NDB.

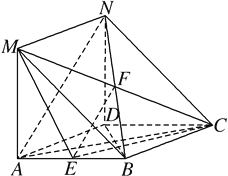
又BN平面NDB，

所以AC⊥BN.

(2)当E为AB的中点时，有AN∥平面MEC.

设CM与BN交于F，连接EF.

由已知可得四边形BCNM是平行四边形，F是BN的中点，

因为E是AB的中点，

所以AN∥EF.

又EF平面MEC，AN平面MEC，

所以AN∥平面MEC.