
历史上有些学者做了成千上万次掷硬币的试验,结果如下表:
| 试验者 | 抛掷次数(n) | 正面向上次数(频数m) | 频率( |
| 棣莫佛 | 2048 | 1061 | 0.5181 |
| 蒲丰 | 4040 | 2048 | 0.5069 |
| 费勒 | 10000 | 4979 | 0.4979 |
| 皮尔逊 | 12000 | 6019 | 0.5016 |
| 皮尔逊 | 24000 | 12012 | 0.5005 |
由上表可知,抛掷硬币试验中,正面向上的概率为( )
A.0.51 B.0.49
C.0.50 D.0.52
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:设计必修一数学(人教A版) 人教A版 题型:044
大约1 500年前,欧洲的数学家们是不知道用“0”的.他们使用罗马数字.罗马数字是用几个表示数的符号,按照一定规则,把它们组合起来表示不同的数目.在这种数字的运用里,不需要“0”这个数字.
而在当时,罗马帝国有一位学者从印度记数法里发现了“0”这个符号.他发现,有了“0”,进行数学运算方便极了,他非常高兴,还把印度人使用“0”的方法向大家做了介绍.过了一段时间,这件事被当时的罗马教皇知道了.当时是欧洲的中世纪,教会的势力非常大,罗马教皇的权利更是远远超过皇帝.教皇非常恼怒,他斥责说,神圣的数是上帝创造的,在上帝创造的数里没有“0”这个怪物,如今谁要把它给引进来,谁就是亵渎上帝!于是,教皇就下令,把这位学者抓了起来,并对他施加了酷刑,用夹子把他的十个手指头紧紧夹住,使他两手残废,让他再也不能握笔写字.就这样,“0”被那个愚昧、残忍的罗马教皇明令禁止了.
但是,虽然“0”被禁止使用,然而罗马的数学家们还是不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”作出了很多数学上的贡献.后来“0”终于在欧洲被广泛使用,而罗马数字却逐渐被淘汰了.
1.科学的发展是曲折的,数学也不例外,针对教皇的行为,谈谈你的看法.
2.真理就是真理,谁也不可能抹杀真理的存在,罗马数学家不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”作出了很多数学上的贡献.同学们面对试图抹杀真理的禁令,你应该怎样做呢?
查看答案和解析>>
科目:高中数学 来源: 题型:
试验者 | 抛掷次数(n) | 正面向上次数(频数m) | 频率( |
棣莫佛 | 2048 | 1061 | 0.5181 |
蒲丰 | 4040 | 2048 | 0.5069 |
费勒 | 10000 | 4979 | 0.4979 |
皮尔逊 | 12000 | 6019 | 0.5016 |
皮尔逊 | 24000 | 12012 | 0.5005 |
由上表可知,抛掷硬币试验中,正面向上的概率为( )
A.0.51 B.0.49
C.0.50 D.0.52
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出两种鱼各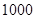 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出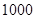 只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了
只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了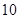 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

(Ⅰ)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;
(Ⅱ)为了估计池塘中鱼的总重量,现从中按照(Ⅰ)的比例对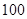 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于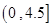 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组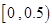 、第二组
、第二组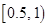 ;……,第九组
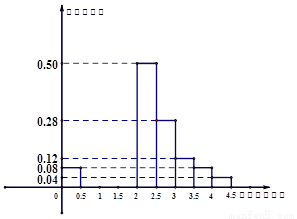
;……,第九组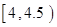 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。
①估计池塘中鱼的重量在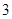 千克以上(含
千克以上(含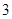 千克)的条数;
千克)的条数;
②若第二组、第三组、第四组鱼的条数依次成公差为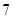 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整;
③在②的条件下估计池塘中鱼的重量的众数、中位数及估计池塘中鱼的总重量;
(Ⅲ)假设随机地从池塘逐只有放回的捕出 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为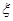 ,求
,求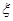 的数学期望。
的数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com