
【题目】已知椭圆C: ![]() +
+ ![]() =1 (a>b>0 ) 经过点 P(1,
=1 (a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
【答案】解:(Ⅰ)由点 ![]() 在椭圆上得,
在椭圆上得, ![]() ①
①
又e= ![]() =
= ![]() ②,c2=a2﹣b2③
②,c2=a2﹣b2③
由①②③得c2=3,a2=4,b2=1,
故椭圆C的标准方程为 ![]() .
.
(Ⅱ)当直线l的斜率不存在,不合题意,可设直线l:y=kx﹣2,P(x1,y1),Q(x2,y2),
将y=kx﹣2代入椭圆方程x2+4y2=4,可得(1+4k2)x2﹣16kx+12=0,
由△=162k2﹣48(1+4k2)>0,解得k> ![]() 或k<﹣
或k<﹣ ![]() .
.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =4
=4 ![]()
![]() ,
,
又O到直线PQ的距离d= ![]() ,
,
则S△OPQ= ![]() d|PQ|=4
d|PQ|=4 ![]() ,
,
设t= ![]() ,(t>0),则4k2=3+t2,
,(t>0),则4k2=3+t2,
即有S△OPQ= ![]() =
= ![]()
由t+ ![]() ≥2
≥2 ![]() =4,
=4,
当且仅当t=2,即k=± ![]()
则S△OPQ≤1.
故△OPQ 面积的最大值为1
【解析】1、由已知可得把点P的坐标代入椭圆的方程,再根据已知的离心率以及椭圆里![]() 联立关于a、b、c的方程即可。
联立关于a、b、c的方程即可。
2、由直线的点斜式和椭圆的方程联立消y可得关于斜率k的方程,直线和椭圆有两个交点即得△>0即得k> ![]() 或k<﹣
或k<﹣ ![]() .再由根与系数的关系得到x1+x2=
.再由根与系数的关系得到x1+x2= ![]() ,x1x2=
,x1x2=![]() ,利用弦长公式求出|PQ|,点到直线的距离求出d即得S△OPQ=
,利用弦长公式求出|PQ|,点到直线的距离求出d即得S△OPQ= ![]() d|PQ|整理这个式子设t=
d|PQ|整理这个式子设t= ![]() ,(t>0)转化成基本不等式的形式求出最小值当且仅当t=2,即k=±
,(t>0)转化成基本不等式的形式求出最小值当且仅当t=2,即k=± ![]() 时等号成立,满足判别式大于0即S△OPQ≤1故△OPQ 面积的最大值为1。
时等号成立,满足判别式大于0即S△OPQ≤1故△OPQ 面积的最大值为1。


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 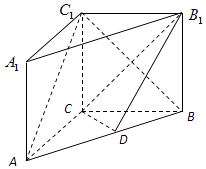
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求二面角B﹣DC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数. (I)函数h(x)=xf (x),当a=l,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(II)记F(x)=f(x)﹣g(x).当a=2,m=0时,若函数F(x)在[﹣1,2]上存在两个不同的零点,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+1=0的圆心在直线ax﹣by+1=0上,则ab的取值范围是( )
A.(﹣∞, ![]() ]
]
B.(﹣∞, ![]() ]
]
C.(0, ![]() ]
]
D.(0, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() ,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
(Ⅰ)求实数m的取值范围;
(Ⅱ)当m=﹣2时,试判断直线l与该圆的位置关系,若相交,求出相应弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( ) 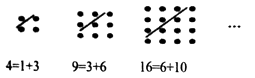
A.16=3+13
B.25=9+16
C.36=10+26
D.49=21+28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.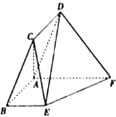
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com