
【题目】已知圆![]() 的圆心坐标
的圆心坐标![]() ,直线
,直线![]() :
:![]() 被圆
被圆![]() 截得弦长为
截得弦长为![]() 。
。
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)从圆![]() 外一点
外一点![]() 向圆引切线,求切线方程。
向圆引切线,求切线方程。
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】试题分析: ![]() 设圆
设圆![]() 的半径为
的半径为![]() ,根据圆心坐标写出圆的标准方程,利用点到直线的距离公式求出圆心到直线
,根据圆心坐标写出圆的标准方程,利用点到直线的距离公式求出圆心到直线![]() 的距离即为弦心距,然后根据垂径定理得到其垂足为弦的中点,由弦长的一半,圆心距及半径构成的直角三角形,根据勾股定理列出关于
的距离即为弦心距,然后根据垂径定理得到其垂足为弦的中点,由弦长的一半,圆心距及半径构成的直角三角形,根据勾股定理列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,从而确定圆
的值,从而确定圆![]() 的方程;
的方程;
![]() 当切线方程的斜率不存在时,显然得到
当切线方程的斜率不存在时,显然得到![]() 为圆的切线;
为圆的切线;
当切线方程的斜率存在时,设出切线的斜率为![]() ,由
,由![]() 的坐标和
的坐标和![]() 写出切线方程,利用点到直线的距离公式求出圆心到所设直线的距离
写出切线方程,利用点到直线的距离公式求出圆心到所设直线的距离![]() ,根据直线与圆相切,得到
,根据直线与圆相切,得到![]() 等于圆的半径,列出关于
等于圆的半径,列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,从而确定出切线的方程,综上,得到所求圆的两条切线方程。
的值,从而确定出切线的方程,综上,得到所求圆的两条切线方程。
解析:(Ⅰ)设圆![]() 的标准方程为:
的标准方程为: ![]()
![]()
圆心![]() 到直线
到直线![]() 的距离:
的距离: ![]() ,
,
则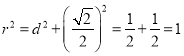
![]() 圆
圆![]() 的标准方程:
的标准方程: ![]()
(Ⅱ)①当切线斜率不存在时,设切线: ![]() ,此时满足直线与圆相切。
,此时满足直线与圆相切。
②当切线斜率存在时,设切线: ![]() ,即
,即![]()
则圆心![]() 到直线
到直线![]() 的距离:
的距离: ![]()
解得: ![]() ,即
,即![]()
则切线方程为: ![]()
综上,切线方程为: ![]() 和
和![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() :
: ![]() 上的一点,椭圆的右焦点为
上的一点,椭圆的右焦点为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 三点互不重合.
三点互不重合.
(1)求椭圆![]() 的方程;
的方程;
(2)求证:直线![]() ,
, ![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中, ![]() 为棱
为棱![]() 上一动点,
上一动点, ![]() 为底面
为底面![]() 上一动点,
上一动点, ![]() 是
是![]() 的中点,若点
的中点,若点![]() 都运动时,点
都运动时,点![]() 构成的点集是一个空间几何体,则这个几何体是( )
构成的点集是一个空间几何体,则这个几何体是( )
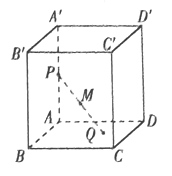
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() ,
,
(1)求圆![]() 方程;
方程;
(2)是否存在过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() (
(![]() 为坐标原点),若存在,求出直线
为坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() 表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)当k=2时,求炮的射程;
(2)求炮的最大射程;
(3)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以其中它?请说明理由.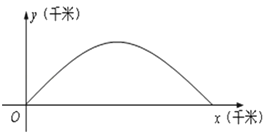
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() 、五合板
、五合板![]() ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓![]() 、五合板
、五合板![]() .出售一张书桌可获利润
.出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=![]() , ∠ABC=60°.
, ∠ABC=60°.
(1)证明:AB⊥A1C;
(2)求二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com