
【题目】设![]() ,函数
,函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若
,若![]() 有两个相异零点
有两个相异零点![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,
时,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)求导,分![]() ,
,![]() 两种情况讨论导函数正负,即得解;
两种情况讨论导函数正负,即得解;
(2)由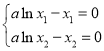 ,构造
,构造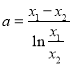 ,结论
,结论![]() ,可转化为
,可转化为
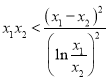 ,构造函数
,构造函数![]() ,分析单调性研究单调性,即可证.
,分析单调性研究单调性,即可证.
(1)![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,则函数
,则函数![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间
![]() 上是增函数.
上是增函数.
综上得:当![]() 时,函数
时,函数![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间;
,无单调递减区间;
当![]() 时,函数
时,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)由题意得,![]() .
.
因为![]() ,
,![]() 是方程
是方程![]() 的两个不同的实数根,所以
的两个不同的实数根,所以
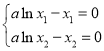 ,两式相减得
,两式相减得![]() ,解得
,解得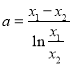 .
.
要证:![]() ,即证:
,即证:![]() ,即证:
,即证: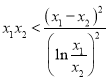 ,
,
即证: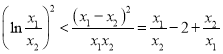 ,
,
令![]() (因为
(因为![]() ),则只需证
),则只需证![]() .
.
设![]() ,∴
,∴![]() ;
;
令![]() ,∴
,∴![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() ,∴
,∴![]() ,
,![]() 在
在![]() 为增函数,
为增函数,![]() .
.
即![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】心理学研究表明,人极易受情绪的影响,某选手参加7局4胜制的兵乒球比赛.
(1)在不受情绪的影响下,该选手每局获胜的概率为![]() ;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到
;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到![]() ;而如果前一局失利的话,此选手该局获胜的概率则降为
;而如果前一局失利的话,此选手该局获胜的概率则降为![]() ,求该选手在前3局获胜局数
,求该选手在前3局获胜局数![]() 的分布列及数学期望;
的分布列及数学期望;
(2)假设选手的三局比赛结果互不影响,且三局比赛获胜的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,求证:
的内角,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,曲线C的参数方程为![]() (a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(a为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点![]() ,l和C交于A,B两点,求
,l和C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司为制定下一年的研发投入计划,需了解年研发资金投入量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 均为常数,
均为常数,![]() 为自然对数的底数.
为自然对数的底数.

现该公司收集了近12年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,
的数据,![]() ,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令![]()
![]()
![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)设![]() 和
和![]() 的相关系数为
的相关系数为![]() ,
,![]() 和
和![]() 的相关系数为
的相关系数为![]() ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;
(2)(i)根据(1的选择及表中数据,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(ii)若下一年销售额![]() 需达到90亿元,预测下一年的研发资金投入量
需达到90亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数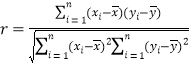 ,回归直线
,回归直线![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: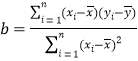 ,
,![]() ;
;
② 参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为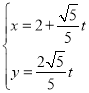 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 交
交![]() 于
于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方),
轴上方),![]() 交极轴于点
交极轴于点![]() (异于极点
(异于极点![]() ).
).
(1)求![]() 的直角坐标方程和
的直角坐标方程和![]() 的直角坐标;
的直角坐标;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上的点,求
上的点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,E是AB的中点,F是BC的中点
(1)求证:EF∥平面A1DC1;
(2)若长方体ABCD﹣A1B1C1D1中,夹在平面A1DC1与平面B1EF之间的几何体的体积为![]() ,求点D到平面B1EF的距离.
,求点D到平面B1EF的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com