
【题目】已知函数![]() ,
, ![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)确定![]() 与
与![]() 的关系;
的关系;
(2)若![]() ,试讨论函数
,试讨论函数![]() 的单调性.
的单调性.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ)由函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴得
轴得![]() ,即
,即![]() ;(Ⅱ)利用第一问
;(Ⅱ)利用第一问![]() ,对二次项系数讨论,结合图像易得函数的单调性.
,对二次项系数讨论,结合图像易得函数的单调性.
试题解析:
(Ⅰ)依题意得![]() ,则
,则![]()
由函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴得:
轴得:
![]()
∴![]()
(Ⅱ)由(Ⅰ)得![]()
![]()
∵函数![]() 的定义域为
的定义域为![]()
∴当![]() 时,
时, ![]()
由![]() 得
得![]() ,由
,由![]() 得
得![]()
即函数![]() 在(0,1)上单调递增,在
在(0,1)上单调递增,在![]() 单调递减
单调递减
当时,令
![]() 得
得![]() 或
或![]()
若![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]()
即函数![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 单调递减
单调递减
若![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]()
即函数![]() 在
在![]() ,
, ![]() 上单调递增,在
上单调递增,在![]() 单调递减
单调递减
若![]() ,即
,即![]() 时,在
时,在![]() 上恒有
上恒有![]()
即函数![]() 在
在![]() 上单调递增
上单调递增
综上得:当![]() 时,函数
时,函数![]() 在(0,1)上单调递增,在
在(0,1)上单调递增,在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;在
单调递减;在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减;在
单调递减;在![]() 上单调递增
上单调递增


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知三次函数的导函数![]() ,
, ![]() ,
, ![]() 为实数.
为实数.
(1)若曲线![]() 在点
在点![]() 处切线的斜率为12,求
处切线的斜率为12,求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上的最小值,最大值分别为
上的最小值,最大值分别为![]() ,1,且
,1,且![]() ,求函数
,求函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
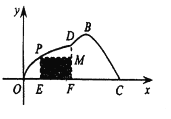
【题目】如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路![]() ,另一侧修建一条休闲大道,它的前一段
,另一侧修建一条休闲大道,它的前一段![]() 是函数
是函数![]() ,
, ![]() 的一部分,后一段
的一部分,后一段![]() 是函数
是函数![]() (
(![]() ,
, ![]() ),
),![]() 时的图象,图象的最高点为
时的图象,图象的最高点为![]() ,
, ![]() ,垂足为
,垂足为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点![]() 落在曲线
落在曲线![]() 上何处时,儿童乐园的面积最大?
上何处时,儿童乐园的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
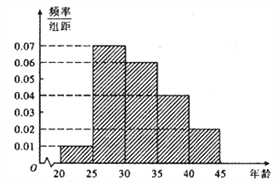
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业有甲、乙两个研发小组.为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a,b),(a,![]() ),(a,b),(
),(a,b),(![]() ,b),(
,b),(![]() ,
,![]() ),(a,b),(a,b),(a,
),(a,b),(a,b),(a,![]() ),(
),(![]() ,b),(a,
,b),(a,![]() ),(
),(![]() ,
,![]() ),(a,b),(a,
),(a,b),(a,![]() ),(
),(![]() ,b),(a,b).其中a,
,b),(a,b).其中a,![]() 分别表示甲组研发成功和失败;b,
分别表示甲组研发成功和失败;b,![]() 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
(I)若某组成功研发一种新产品,则给该组记1分,否则记0分.试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(II)若该企业安排甲、乙两组各自研发一种新产品,试估计恰有一组研发成功的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com