
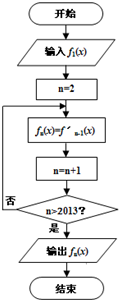
 右程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数.若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为
右程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数.若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 已知用户甲的电脑被某黑客乙入侵.黑客乙为了窃取甲的某重要帐户的用户名和密码,在甲的电脑中植入了如右程序框图所示的电脑程序,在甲每次登陆其重要帐户之前,电脑先执行此程序,让甲输入其用户名a,密码d和一个随机的验证码k(a、d、k均为正实数),因为甲的用户名和密码受到保护,所以乙每次只能看到验证码k和输出结果S.某一天甲登陆了两次其重要帐户,乙看当到k=2时S=
已知用户甲的电脑被某黑客乙入侵.黑客乙为了窃取甲的某重要帐户的用户名和密码,在甲的电脑中植入了如右程序框图所示的电脑程序,在甲每次登陆其重要帐户之前,电脑先执行此程序,让甲输入其用户名a,密码d和一个随机的验证码k(a、d、k均为正实数),因为甲的用户名和密码受到保护,所以乙每次只能看到验证码k和输出结果S.某一天甲登陆了两次其重要帐户,乙看当到k=2时S=| 1 |
| 3 |
| 4 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
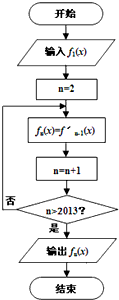 右程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数.若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为________.
右程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数.若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为________.查看答案和解析>>
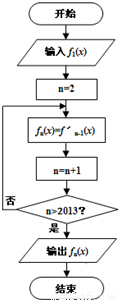
科目:高中数学 来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷16(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com