练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线（为参数），曲线（为参数），以坐标原点为极点， 轴的正半轴为极轴建立直角坐标系.

    （1）求曲线的极坐标方程，直线的普通方程；

    （2）把直线向左平移一个单位得到直线，设与曲线的交点为， ， 为曲线上任意一点，求面积的最大值.

    【答案】（1）， ；（2）

    【解析】试题分析：（1）由，消去参数即可得直线的普通方程，由， ，代入可得曲线的极坐标方程；

    （2）把直线向左平移一个单位得到直线的方程为，其极坐标方程为，与曲线的极坐标方程联立得，由韦达定理计算，圆心到直线的距离为加上半径可得最大距离，从而得最大面积.

    试题解析：

    （1）把曲线消去参数可得，

    令， ，代入可得曲线的极坐标方程为.

    把直线化为普通方程.

    （2）把直线向左平移一个单位得到直线的方程为，其极坐标方程为.

    联立所以，所以

    故.

    圆心到直线的距离为，

    圆上一点到直线的最大距离为，

    所以面积的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列四个命题：

    ① 函数与函数表示同一个函数．

    ② 奇函数的图象一定过直角坐标系的坐标原点．

    ③ 函数的图象可由的图象向左平移个单位长度得到．

    ④ 若函数的定义域为，则函数的定义域为．

    其中正确命题的序号是_________ (填上所有正确命题的序号) ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某蛋糕店制作并销售一款蛋糕，当天每售出个获得利润元，未售出的每个亏损元.根据以往天的资料统计，得到如下需求量表.元日这天，此蛋糕店制作了这款蛋糕个.以（单位：个， ）表示这天的市场需求量. （单位：元）表示这天出售这款蛋糕获得的利润.

    需求量/个

    天数

    15

    25

    30

    20

    10

    （1）当时，若时获得的利润为， 时获得的利润为，试比较和的大小；

    （2）当时，根据上表，从利润不少于元的天数中，按需求量分层抽样抽取天，

    （ⅰ）求这天中利润为元的天数；

    （ⅱ）再从这天中抽取天做进一步分析，设这天中利润为元的天数为，求随机变量的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某蛋糕店制作并销售一款蛋糕，当天每售出个利润为元，未售出的每个亏损元.根据以往天的统计资料，得到如下需求量表，元旦这天，此蛋糕店制作了个这种蛋糕.以（单位：个， ）表示这天的市场需求量. （单位：元）表示这天售出该蛋糕的利润.

    需求量/个

    天数

    10

    20

    30

    25

    15

    （1）将表示为的函数，根据上表，求利润不少于元的概率；

    （2）估计这天的平均需求量（同一组数据用该区间的中点值作代表）；

    （3）元旦这天，该店通过微信展示打分的方式随机抽取了名市民进行问卷调查，调查结果如下表所示，已知在购买意愿强的市民中，女性的占比为.

    购买意愿强

    购买意愿弱

    合计

    女性

    28

    男性

    22

    合计

    28

    22

    50

    完善上表，并根据上表，判断是否有的把握认为市民是否购买这种蛋糕与性别有关？

    附： .

    0.05

    0.025

    0.010

    0.005

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中非毕业班学生人数分布情况如下表，为了了解这2000个学生的体重情况，从中随机抽取160个学生并测量其体重数据，根据测量数据制作了下图所示的频率分布直方图.

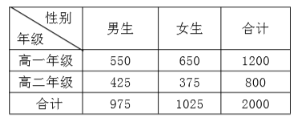
    （1）为了使抽取的160个样品更具代表性，宜采取分层抽样，请你给出一个你认为合适的分层抽样方案，并确定每层应抽取的样品个数；

    （2）根据频率分布直方图，求的值，并估计全体非毕业班学生中体重在内的人数；

    （3）已知高一全体学生的平均体重为，高二全体学生的平均体重为，试估计全体非毕业班学生的平均体重.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，，，点在棱上移动．

    （1）证明：；

    （2）求直线与平面所成的角；

    （3）当为的中点时，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区对一种新品种小麦在一块试验田进行试种.从试验田中抽取株小麦，测量这些小麦的生长指标值，由测量结果得如下频数分布表：

    生长指标值分组

    频数

    （1）在相应位置上作出这些数据的频率分布直方图；

    （2）求这株小麦生长指标值的样本平均数和样本方差（同一组中的数据用该组区间的中点值作代表）；

    （3）由直方图可以认为，这种小麦的生长指标值服从正态分布，其中近似为样本平均数， 近似为样本方差.

    ①利用该正态分布，求；

    ②若从试验田中抽取株小麦，记表示这株小麦中生长指标值位于区间的小麦株数，利用①的结果，求.

    附： .

    若，则，

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P－ABCD的底面为直角梯形，AD∥BC，AD＝2BC＝2，BC⊥DC，∠BAD＝60°，平面PAD⊥底面ABCD，E为AD的中点，△PAD为正三角形，M是棱PC上的一点(异于端点)．

    (1)若M为PC的中点，求证：PA∥平面BME；

    (2)是否存在点M，使二面角MBED的大小为30°.若存在，求出点M的位置；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），将曲线上各点的横坐标都缩短为原来的倍，纵坐标坐标都伸长为原来的倍，得到曲线，在极坐标系（与直角坐标系取相同的单位长度，且以原点为极点，以轴非负半轴为极轴）中，直线的极坐标方程为．

    （1）求直线和曲线的直角坐标方程；

    （2）设点是曲线上的一个动点，求它到直线的距离的最大值．

    查看答案和解析>>

    同步练习册答案