
已知实数 ,函数
,函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)当 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形.
(1)2;(2)递增;(3)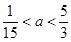 .
.
解析试题分析:(1)研究函数问题,一般先研究函数的性质,如奇偶性,单调性,周期性等等,如本题中函数 是偶函数,因此其最小值我们只要在
是偶函数,因此其最小值我们只要在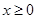 时求得即可;(2)
时求得即可;(2) 时,
时, 可化简为
可化简为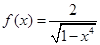 ,下面我们只要按照单调性的定义就可证明在
,下面我们只要按照单调性的定义就可证明在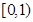 上函数是单调递增的,当然在
上函数是单调递增的,当然在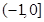 上是递减的;(3)处理此问题,首先通过换元法把问题简化,设
上是递减的;(3)处理此问题,首先通过换元法把问题简化,设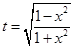 ,则函数
,则函数 变为
变为 ,问题变为求实数
,问题变为求实数 的范围,使得在区间
的范围,使得在区间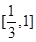 上,恒有
上,恒有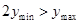 .对于函数
.对于函数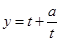 ,我们知道,它在
,我们知道,它在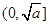 上递减,在
上递减,在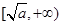 上递增,故我们要讨论它在区间
上递增,故我们要讨论它在区间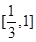 上的最大(小)值,就必须分类讨论,分类标准显然是
上的最大(小)值,就必须分类讨论,分类标准显然是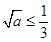 ,
,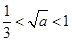 ,
,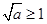 ,在
,在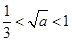 时还要讨论最大值在区间
时还要讨论最大值在区间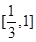 的哪个端点取得,也即共分成四类.
的哪个端点取得,也即共分成四类.
试题解析:易知 的定义域为
的定义域为 ,且
,且 为偶函数.
为偶函数.
(1) 时,
时,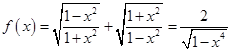 2分
2分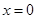 时
时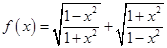 最小值为2. 4分
最小值为2. 4分
(2) 时,
时,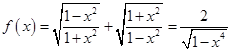
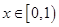 时,
时,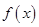 递增;
递增;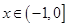 时,
时,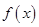 递减; 6分
递减; 6分 为偶函数.所以只对
为偶函数.所以只对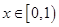 时,说明
时,说明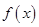 递增.
递增.
设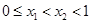 ,所以
,所以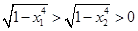 ,得
,得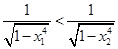
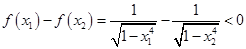
所以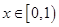 时,
时,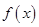 递增; 10分
递增; 10分
(3)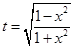 ,
,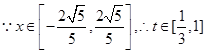 ,
,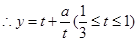
从而原问题等价于求实数 的范围,使得在区间
的范围,使得在区间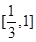 上,
上,
恒有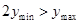 . 11分
. 11分
①当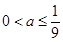 时,
时,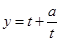 在
在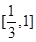 上单调递增,
上单调递增,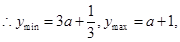 由
由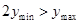 得
得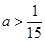 ,
,
从而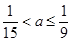 ; 12分
; 12分
②当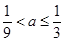 时,
时,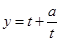 在
在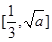 上单调递减,在
上单调递减,在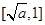 上单调递增,
上单调递增,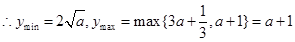 ,
,
由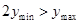 得
得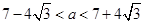 ,从而
,从而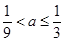 ; 13分
; 13分
③当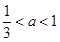 时,
时,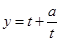 在
在

科目:高中数学 来源: 题型:解答题
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数 与第x天近似地满足
与第x天近似地满足 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费 近似地满足
近似地满足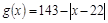 (元).
(元).
(1)求该村的第x天的旅游收入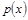 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,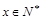 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com