
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
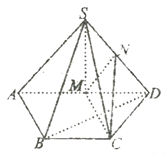
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() .
.
【答案】详见解析
【解析】试题分析:证明线面平行有两种思路:第一寻求线线平行,利用线面平行的判定定理.第二寻求面面平行,本题借助平行四边形和三角形中位线定理可以得到线线平行,进而证明线面平行;证明线面垂直,第一可利用线面垂直的判定定理,证明直线与平面内的两条相交直线垂直,进而说明线面垂直.第二可建立空间直角坐标系,写出向量的坐标,借助空间向量解题,利用两个向量数量积为零,说明线线垂直,也是很简单的做法.
试题解析:
证明:(1)设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
, ![]() .
.
因为![]() ,且
,且![]() ,
, ![]() 为
为![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,且
,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
在平行四边形![]() 中,因为
中,因为![]() ,所以四边形
,所以四边形![]() 为菱形,所以
为菱形,所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线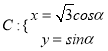 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的机坐标系中,直线
轴的非负半轴为极轴建立的机坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家治理环境污染的号召,增强学生的环保意识,宿州市某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了l00学生的成绩进行统计,成绩频率分布直方图如图所示.估计这次测试中成绩的众数为;平均数为;中位数为 . (各组平均数取中值计算,保留整数) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过抛物线C的焦点,且与C的对称轴垂直.l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )
A.18
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y= ![]() cos(
cos( ![]() ﹣2x)的单调递增区间是( )
﹣2x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ﹣ ![]() ,kπ)(k∈Z)
,kπ)(k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ+ ![]() ,kπ+π](k∈Z)
,kπ+π](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点O,![]() 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为![]() ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为![]() ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜率为1的直线过抛物线y2=2px(p>0)的焦点,与抛物线交于两点A、B,M为抛物线 ![]() 上的动点.
上的动点. 
(1)若|AB|=8,求抛物线的方程;
(2)求S△ABM的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com