

| (1)证明:由直四棱柱,得BB1∥DD1,且BB1=DD1, 所以,BB1D1D是平行四边形, 所以,B1D1∥BD, 而BD 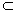 平面A1BD,B1D1 平面A1BD,B1D1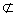 平面A1BD, 平面A1BD,所以B1D1∥平面A1BD. (2)证明:因为BB1⊥面ABCD,AC 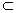 面ABCD, 面ABCD,所以BB1⊥AC, 又因为BD⊥AC,且BD∩BB1=B, 所以,AC⊥面BB1D, 而MD 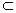 面BB1D, 面BB1D,所以MD⊥AC. |
|
| (3)解:当点M为棱BB1的中点时,平面DMC1⊥平面CC1D1D, 取DC的中点N,D1C1的中点N1, 连结NN1交DC1于O,连结OM, 因为N是DC中点,BD=BC, 所以,BN⊥DC; 又因为DC是面ABCD与 面DCC1D1的交线, 而面ABCD⊥面DCC1D1, 所以,BN⊥面DCC1D1, 又可证得,O是NN1的中点, 所以,BM∥ON且BM=ON,即BMON是平行四边形, 所以,BN∥OM, 所以,OM⊥平面CC1D1D, 因为OM  面DMC1, 面DMC1,所以,平面DMC1⊥平面CC1D1D. |
 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
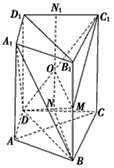
 19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
19、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点.
18、如图所示,在直四棱柱ABCD-A1B1C1D1中,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.
16、如图所示,在直四棱柱M中,DB=BC,MN,点EN是棱MN上一点.查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习巩固与练习:空间中的垂直关系(解析版) 题型:解答题
 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com