
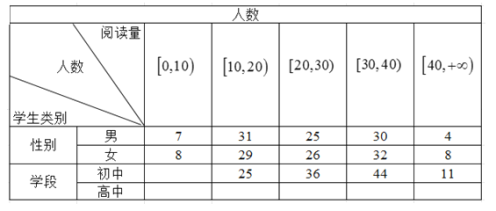
【题目】为了解中学生课外阅读情况,现从某中学随机抽取![]() 名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
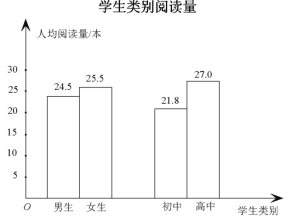
下面有四个推断:
①这![]() 名学生阅读量的平均数可能是
名学生阅读量的平均数可能是![]() 本;
本;
②这![]() 名学生阅读量的
名学生阅读量的![]() 分位数在区间
分位数在区间![]() 内;
内;
③这![]() 名学生中的初中生阅读量的中位数一定在区间
名学生中的初中生阅读量的中位数一定在区间![]() 内;
内;
④这![]() 名学生中的初中生阅读量的
名学生中的初中生阅读量的![]() 分位数可能在区间
分位数可能在区间![]() 内.
内.
所有合理推断的序号是________.
【答案】②③④
【解析】
①由学生类别阅读量图表可知;
②计算75%分位数的位置,在区间内查人数即可;
③设在区间![]() 内的初中生人数为
内的初中生人数为![]() ,则
,则![]() ,分别计算
,分别计算![]() 为最大值和最小值时的中位数位置即可;
为最大值和最小值时的中位数位置即可;
④设在区间![]() 内的初中生人数为
内的初中生人数为![]() ,则
,则![]() ,分别计算
,分别计算![]() 为最大值和最小值时的25%分位数位置即可.
为最大值和最小值时的25%分位数位置即可.
在①中,由学生类别阅读量中男生和女生人均阅读量知,这200名学生的平均阅读量在区间![]() 内,故错误;
内,故错误;
在②中,![]() ,阅读量在
,阅读量在![]() 的人数有
的人数有![]() 人,
人,
在![]() 的人数有62人,所以这200名学生阅读量的75%分位数在区间
的人数有62人,所以这200名学生阅读量的75%分位数在区间![]() 内,
内,
故正确;
在③中,设在区间![]() 内的初中生人数为
内的初中生人数为![]() ,则
,则![]() ,
,
当![]() 时,初中生总人数为116人,
时,初中生总人数为116人,![]() ,
,
此时区间![]() 有25人,区间
有25人,区间![]() 有36人,所以中位数在
有36人,所以中位数在![]() 内,
内,
当![]() 时,初中生总人数为131人,
时,初中生总人数为131人,![]() ,
,
区间![]() 有
有![]() 人,区间
人,区间![]() 有36人,所以中位数在
有36人,所以中位数在![]() 内,
内,
当区间![]() 人数去最小和最大,中位数都在
人数去最小和最大,中位数都在![]() 内,
内,
所以这![]() 名学生中的初中生阅读量的中位数一定在区间
名学生中的初中生阅读量的中位数一定在区间![]() 内,故正确;
内,故正确;
在④中,设在区间![]() 内的初中生人数为
内的初中生人数为![]() ,则
,则![]() ,
,
当![]() 时,初中生总人数为116人,
时,初中生总人数为116人,![]() ,
,
此时区间![]() 有25人,区间
有25人,区间![]() 有36人,所以25%分位数在
有36人,所以25%分位数在![]() 内,
内,
当![]() 时,初中生总人数为131人,
时,初中生总人数为131人,![]() ,
,
区间![]() 有
有![]() 人,所以25%分位数在
人,所以25%分位数在![]() 内,
内,
所以这![]() 名学生中的初中生阅读量的25%分位数可能在区间
名学生中的初中生阅读量的25%分位数可能在区间![]() 内,故正确;
内,故正确;
故答案为:②③④


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PCD⊥平面ABCD,![]() ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,![]() .
.
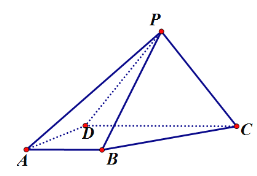
(1)求证:平面PAD⊥平面PBC;
(2)求直线PB与平面PAD所成的角;
(3)在棱PC上是否存在一点E使得直线![]() 平面PAD,若存在求PE的长,并证明你的结论.
平面PAD,若存在求PE的长,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓缓爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到了终点.用![]() 和
和![]() 分别表示乌龟和兔子经过时间t所行的路程,则下列图象中与故事情节相吻合的是( )
分别表示乌龟和兔子经过时间t所行的路程,则下列图象中与故事情节相吻合的是( )
A.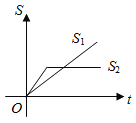 B.
B.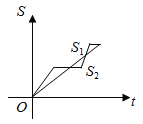
C.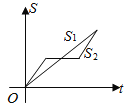 D.
D.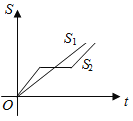
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果f(x)是定义在R上的函数,且对任意的x∈R,均有f(-x)≠-f(x),则称该函数是“X—函数”.
(1)分别判断下列函数:①y=![]() ;②y=x+1;③y=x2+2x-3是否为“X—函数”?(直接写出结论)
;②y=x+1;③y=x2+2x-3是否为“X—函数”?(直接写出结论)
(2)若函数f(x)=x-x2+a是“X—函数”,求实数a的取值范围;
(3)设“X—函数”f(x)=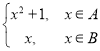 在R上单调递增,求所有可能的集合A与B.
在R上单调递增,求所有可能的集合A与B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=log2(kx2+4kx+3).①若f(x)的定义域为R,则k的取值范围是_____;②若f(x)的值域为R,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
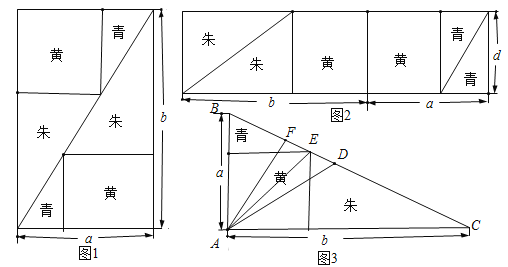
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于![]() 的说法,正确的是( )
的说法,正确的是( )
A.展开式中的二项式系数之和为2048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() ,
,![]() 三班共有140名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时)
三班共有140名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时)
| 6.5 | 7 | 7.5 | |||
| 7 | 8 | 9 | 10 | 11 | |
| 4.5 | 6 | 7.5 | 9 | 10.5 | 12 |
(1)试估计![]() 班的学生人数;
班的学生人数;
(2)从![]() 班和
班和![]() 班抽出的人数中,各随机选取一人,
班抽出的人数中,各随机选取一人,![]() 班选出的人记为甲,
班选出的人记为甲,![]() 班选出的人记为乙,假设所有学生锻炼时间互不影,求该周甲锻炼时间比乙的锻炼时间长的概率;
班选出的人记为乙,假设所有学生锻炼时间互不影,求该周甲锻炼时间比乙的锻炼时间长的概率;
(3)再从![]() ,
,![]() ,
,![]() 三班中各随机抽取一名学生,设新抽取的学生该周锻炼时间分别为7,9,8.25(单位:小时),这3个新数据与表格构成的新样本的平均数记为
三班中各随机抽取一名学生,设新抽取的学生该周锻炼时间分别为7,9,8.25(单位:小时),这3个新数据与表格构成的新样本的平均数记为![]() ,表格中数据的平均数记为
,表格中数据的平均数记为![]() ,试判断
,试判断![]() 和
和![]() 的大小(结论不需要证明).
的大小(结论不需要证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com