
【题目】已知数列![]() 中,
中, ![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 是等差数列,写出
是等差数列,写出![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式及数列
的通项公式及数列![]() 中的最大项与最小项.
中的最大项与最小项.
【答案】(1)详见解析;(2)![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ)首先通过已知条件![]() 化简变形,凑出
化简变形,凑出![]() 这种形式,凑出
这种形式,凑出![]() 常数,
常数,
就可以证明数列![]() 是等差数列,并利用等差数列的通项公式求出
是等差数列,并利用等差数列的通项公式求出![]() 通项公式;(Ⅱ)因为
通项公式;(Ⅱ)因为![]() 与
与![]() 有关,所以利用
有关,所以利用![]() 的通项公式求出数列
的通项公式求出数列![]() 的通项公式,把通项公式看成函数,利用函数图像求最大值和最小值.
的通项公式,把通项公式看成函数,利用函数图像求最大值和最小值.
试题解析:(Ⅰ)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴数列
,∴数列![]() 是以1为公差的等差数列. 4分
是以1为公差的等差数列. 4分
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
, ![]() ,
,
∴![]() 是以
是以![]() 为首项,
为首项, ![]() 为公差的等差中项.
为公差的等差中项.
∴![]() ,
, ![]() . 7分
. 7分
(Ⅱ)∵![]() ,
,  ,
, ![]() .
.
∴作函数 的图像如图所示:
的图像如图所示:

∴由图知,在数列![]() 中,最大项为
中,最大项为![]() ,最小项为
,最小项为![]() . 13分
. 13分
另解: ,当
,当![]() 时,数列
时,数列![]() 是递减数列,且
是递减数列,且![]() .
.
列举![]() ;
;![]() ;
;![]() .所以在数列
.所以在数列![]() 中,最大项为
中,最大项为![]() ,最小项为
,最小项为![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②从含有2008个个体的总体中抽取一个容量为100的样本,现采用系统抽样方法应先剔除8人,则每个个体被抽到的概率均为![]() ;
;
③从总体中抽取的样本数据共有m个a,n个b,p个c,则总体的平均数![]() 的估计值为
的估计值为![]() ;
;
④某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中真命题的个数是 _____个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 与定点
与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离的比是
的距离的比是![]() ∶
∶![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)对于定点![]() ,作过点
,作过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,求△
,求△![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[ ![]() ,
, ![]() ],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( ) 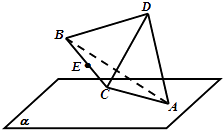
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com