
【题目】为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如表:
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(Ⅰ)求y关于x的线性回归方程 ![]() ;
;
(Ⅱ)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式: ![]() =
= 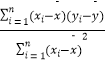 =
= 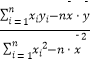 ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,已知O为△ABC的外心,角A、B、C的对边分别为a、b、c.
(1)若5 ![]() +4
+4 ![]() +3
+3 ![]() =
= ![]() ,求cos∠BOC的值;
,求cos∠BOC的值;
(2)若 ![]()
![]() =
= ![]()
![]() ,求
,求 ![]() 的值.
的值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列向量组中能作为表示它们所在平面内所有向量的基底的是( )
A.![]() =(0,0),
=(0,0), ![]() =(1,﹣2)
=(1,﹣2)
B.![]() =(﹣1,2),
=(﹣1,2), ![]() =(2,﹣4)
=(2,﹣4)
C.![]() =(3,5),
=(3,5), ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(6,9)
=(6,9)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足Sn= ![]() an﹣n(t>0且t≠1,n∈N*)
an﹣n(t>0且t≠1,n∈N*)
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式(用t,n表示)
(2)当t=2时,令cn= ![]() ,证明
,证明 ![]() ≤c1+c2+c3+…+cn<1.
≤c1+c2+c3+…+cn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足 ![]() ,n∈N* . (Ⅰ)求数列{an}的通项公式;
,n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 若不等式Sn>kan﹣2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人投篮的水平都比较稳定,若三人各自独立地进行一次投篮测试,则甲投中而乙不投中的概率为 ![]() ,乙投中而丙不投中的概率为
,乙投中而丙不投中的概率为 ![]() ,甲、丙两人都投中的概率为
,甲、丙两人都投中的概率为 ![]() .
.
(1)分别求甲、乙、丙三人各自投篮一次投中的概率;
(2)若丙连续投篮5次,求恰有2次投中的概率;
(3)若丙连续投篮3次,每次投篮,投中得2分,未投中得0分,在3次投篮中,若有2次连续投中,而另外1次未投中,则额外加1分;若3次全投中,则额外加3分,记ξ为丙连续投篮3次后的总得分,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点,求证: (Ⅰ)PA∥平面EDB
(Ⅱ)AD⊥PC.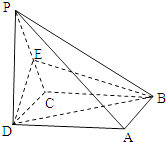
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点F1(﹣c,0),F2(c,0),椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,若椭圆与双曲线的离心率分别为e1 , e2 , 则3e12+e22的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com