
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
(I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
(II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
参考公式: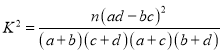 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
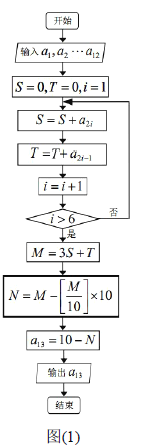
【题目】条形码是由一组规则排列的条、空及其对应的代码组成,用来表示一定的信息,我们通常见的条形码是“![]() ”通用代码,它是由从左到右排列的
”通用代码,它是由从左到右排列的![]() 个数字(用
个数字(用![]() ,
,![]() ,…,
,…,![]() 表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中
表示)组成,这些数字分别表示前缀部分、制造厂代码、商品代码和校验码,其中![]() 是校验码,用来校验前
是校验码,用来校验前![]() 个数字代码的正确性.图(1)是计算第
个数字代码的正确性.图(1)是计算第![]() 位校验码的程序框图,框图中符号
位校验码的程序框图,框图中符号![]() 表示不超过
表示不超过![]() 的最大整数(例如
的最大整数(例如![]() ).现有一条形码如图(2)所示(
).现有一条形码如图(2)所示(![]() ),其中第
),其中第![]() 个数被污损,那么这个被污损数字
个数被污损,那么这个被污损数字![]() 是( )
是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com