练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在等差数列{an}中，2a9＝a12+13，a3＝7，其前n项和为Sn．

    （1）求数列{an}的通项公式；

    （2）求数列{}的前n项和Tn，并证明Tn＜．

    【答案】（1）（2）见解析

    【解析】

    （1）等差数列{an}的公差设为d，运用等差数列的通项公式，解方程可得首项和公差，进而得到所求通项公式；

    （2）运用等差数列的求和公式，求得（），再由数列的裂项相消求和可得Tn，再由不等式的性质即可得证．

    （1）等差数列{an}的公差设为d，2a9＝a12+13，a3＝7，

    可得2（a1+8d）＝a1+11d+13，a1+2d＝7，

    解得a1＝3，d＝2，

    则an＝3+2（n﹣1）＝2n+1；

    （2）Snn（3+2n+1）＝n（n+2），

    （），

    前n项和Tn（1）

    （1）（）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线上的任意一点到两定点、距离之和为，直线交曲线于两点，为坐标原点．

    （1）求曲线的方程；

    （2）若不过点且不平行于坐标轴，记线段的中点为，求证：直线的斜率与的斜率的乘积为定值；

    （3）若直线过点，求面积的最大值，以及取最大值时直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的定义域为，部分对应值如下表，又知的导函数的图象如下图所示：

    -1

    0

    4

    5

    1

    2

    2

    1

    则下列关于的命题：

    ①为函数的一个极大值点；

    ②函数的极小值点为2；

    ③函数在上是减函数；

    ④如果当时，的最大值是2，那么的最大值为4；

    ⑤当时，函数有4个零点.

    其中正确命题的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆经过，，三点．

    (1)求圆的标准方程；

    (2)若过点N 的直线被圆截得的弦AB的长为，求直线的倾斜角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}：1，﹣2，﹣2，3，3，3，﹣4，﹣4，﹣4，﹣4，…， ，…，即当 ＜n≤ （k∈N*）时， ．记Sn=a1+a2+…+an（n∈N）．对于l∈N ， 定义集合Pl=﹛n|Sn为an的整数倍，n∈N ， 且1≤n≤l}
    （1）求P11中元素个数；
    （2）求集合P2000中元素个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年6月14日，世界杯足球赛在俄罗斯拉开帷幕.通过随机调查某小区100名性别不同的居民是否观看世界杯比赛，得到以下列联表：

    观看世界杯

    不观看世界杯

    总计

    男

    40

    20

    60

    女

    15

    25

    40

    总计

    55

    45

    100

    经计算的观测值.

    附表：

    0.05

    0.025

    0.010

    0.005

    0.001

    3.841

    5.024

    6.635

    7.879

    10.828

    参照附表，所得结论正确的是（ ）

    A. 有以上的把握认为“该小区居民是否观看世界杯与性别有关”

    B. 有以上的把握认为“该小区居民是否观看世界杯与性别无关”

    C. 在犯错误的概率不超过0.005的前提下，认为“该小区居民是否观看世界杯与性别有关”

    D. 在犯错误的概率不超过0.001的前提下，认为“该小区居民是否观看世界杯与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《厉害了，我的国》这部电影记录：到2017年底，我国高铁营运里程达2.5万公里，位居世界第一位，超过第二名至第十名的总和，约占世界高铁总量的三分之二.如图是我国2009年至2017年高铁营运里程（单位：万公里）的折线图.

    根据这9年的高铁营运里程，甲、乙两位同学分别选择了与时间变量的两个回归模型①：；②.

    （1）求，（精确到0.01）；

    （2）乙求得模型②的回归方程为，你认为哪个模型的拟合效果更好？并说明理由.

    附：参考公式：，，.

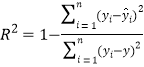    参考数据：

    1.39

    76.94

    285

    0.22

    0.09

    3.72

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞0，函数 ．
    （1）记f（x）在区间[0，4]上的最大值为g（a），求g（a）的表达式；
    （2）是否存在a使函数y=f（x）在区间（0，4）内的图象上存在两点，在该两点处的切线互相垂直？若存在，求出a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设,函数在区间上单调递增，在区间上单调递减.

    （Ⅰ）若，求的值；

    （Ⅱ）求函数在区间上的最小值（用表示）.

    查看答案和解析>>

    同步练习册答案