
【题目】如图,正方体![]() 的棱长为2,
的棱长为2,![]() 分别为
分别为![]() 的中点,则以下说法错误的是( )
的中点,则以下说法错误的是( )
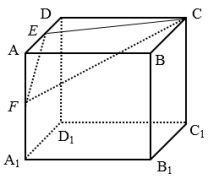
A.平面![]() 截正方体所的截面周长为
截正方体所的截面周长为![]()
B.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
C.三棱锥![]() 和
和![]() 体积相等
体积相等
D.存在![]() 上一点
上一点![]() 使得
使得![]() 平面
平面![]()
【答案】B
【解析】
对于A,平面![]() 截正方体所得的截面为梯形
截正方体所得的截面为梯形![]() ,求出梯形的周长即可得解;
,求出梯形的周长即可得解;
对于B,通过建立空间直角坐标系,设出![]() 点坐标,证出
点坐标,证出![]() 不成立,即可得出B选项错误;
不成立,即可得出B选项错误;
对于C,通过等体积法,分别求出三棱锥![]() 和
和![]() 的体积,进而得解;
的体积,进而得解;
对于D,通过线线平行,证得线面平行,进而得解.
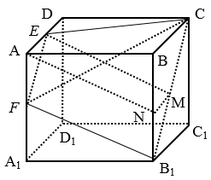
对于A选项,连接![]() ,
,![]() ,
,
![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() 四点共线,
四点共线,
![]() 平面
平面![]() 截正方体所得的截面为梯形
截正方体所得的截面为梯形![]() ,
,
![]() 截面周长
截面周长![]() ,
,
故A正确;
对于B选项,建立如图所示的空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
所以![]() ,
,![]() ,
,
若![]() 平面
平面![]() ,则
,则![]() ,而
,而![]() 显然不成立,
显然不成立,
所以![]() 与
与![]() 不垂直,所以
不垂直,所以![]() 上不存在点
上不存在点![]() ,使得
,使得![]() 平面
平面![]() ,
,
所以B选项错误;
对于C选项,
![]() ,
,
![]() ,
,
所以![]() 成立,C正确;
成立,C正确;
对于D选项,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]() 点
点![]() 为
为![]() 的中点,
的中点,
![]()
![]() 上存在一点
上存在一点![]() 使得
使得![]() 平面
平面![]() ,故D正确.
,故D正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球(取出某色球的概率均相同),确定颜色后放回,直到连续两次均取出红色球时为止,记此时取出球的次数为ξ,则ξ的数学期望为_____ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,其图象关于直线
,其图象关于直线![]() 对称.给出下面四个结论:①将
对称.给出下面四个结论:①将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数图象关于原点对称;②点
个单位长度后得到函数图象关于原点对称;②点![]() 为
为![]() 图象的一个对称中心;③
图象的一个对称中心;③![]() ;④
;④![]() 在区间
在区间![]() 上单调递增.其中正确的结论为( )
上单调递增.其中正确的结论为( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线l经过点![]() ,且与椭圆
,且与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() (
(![]() 为坐标原点)成等比数列,判断直线
为坐标原点)成等比数列,判断直线![]() 的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为A,B,C,D,E五个等级.某试点高中2019年参加“选择考”总人数是2017年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2017年和2019年“选择考”成绩等级结果,得到如图表:


针对该校“选择考”情况,2019年与2017年比较,下列说法正确的是( )
A.获得A等级的人数不变B.获得B等级的人数增加了1倍
C.获得C等级的人数减少了D.获得E等级的人数不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式,此事引起了国际数学界的轰动许多专家认为这是数论研究中的一项重大突破世界主流媒体都对这项重要成果作了报道并给予了高度评价,印度媒体甚至称赞张益唐为“中国的拉马努金”.孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,素数对
是素数,素数对![]() 称为孪生素数.在不超过20的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )
称为孪生素数.在不超过20的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系内,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 和直线
和直线![]() 化为直角坐标方程;
化为直角坐标方程;
(2)过原点![]() 引一条射线分别交曲线
引一条射线分别交曲线![]() 和直线
和直线![]() 于
于![]() ,
,![]() 两点,射线上另有一点
两点,射线上另有一点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程(写成直角坐标形式的普通方程).
的轨迹方程(写成直角坐标形式的普通方程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com