Question

【题目】已知函数为奇函数．

(1)求常数的值；

(2)设，证明函数在(1，＋∞)上是减函数；

(3)若函数，且在区间[3,4]上没有零点，求实数的取值范围.

Answer 1

【答案】（1）；（2）m>或m<－.

【解析】试题分析：（1）由于为奇函数，可得，即可得出；（2）利用对数函数的单调性和不等式的性质通过作差即可得出；（3）利用（2）函数的单调性、指数函数的单调性即可得出.

试题解析：∵f(x)＝为奇函数

∴f(－x)＝－f(x)，即＝－＝，

∴，即1－k2x2＝1－x2，整理得k2＝1.

∴k＝－1(k＝1使f(x)无意义而舍去)．

(2)证明：由(1)得，k＝－1，h(x)＝，任取x1，x2∈(1，＋∞)，且x1<x2，

则h(x2)－h(x1)＝＝.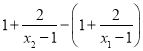

∵x1，x2∈(1，＋∞)，且x1<x2，

∴x1－x2<0，x1－1>0，x2－1>0，

∴h(x2)－h(x1)＝，

∴h(x1)>h(x2)，

∴函数y＝h(x)在(1，＋∞)是减函数．

(3)解：由(2)知，f(x)在(1，＋∞)上递增，

∴g(x)＝f(x)—＋m在[3,4]递增．

∵g(x)在区间[3,4]上没有零点．

∴g(3)＝－＋m＝＋m>0或g(4)＝－＋m＝， ＋m<0，

∴m>或m<－.