
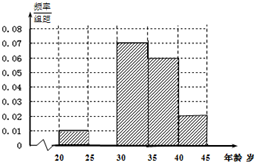
 (2012•佛山一模)某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
(2012•佛山一模)某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| 0.10 |
| 0.07 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| R | 2 n |
| x |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 7 |
| 5 |
| Sn-2n |
| Tn |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 合唱社 | 粤曲社 | 书法社 | |
| 高一 | 45 | 30 | a |
| 高二 | 15 | 10 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•佛山一模)如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
(2012•佛山一模)如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com