
| (a-x)2+(b-x) 2 -(c-x) 2 |
| 2(a-x)(b-x) |


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
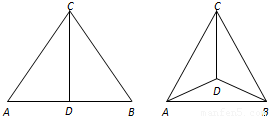
 如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
 ⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑵试在平面ABC上确定一点P,使DP与平面ABC内任意一条直线垂直,证明你的结论.
⑶如果在折成的三棱锥内有一个小球,求出球的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,一个等腰直角三角形的硬纸片△ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高,沿CD把△ABC折成直二面角.
 ⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑴如果你手中只有一把能够量长度的直尺,应该如何确定A、B的位置,使得二面角A—CD—B是直二面角?证明你的结论.
⑵试在平面ABC上确定一点P,使DP与平面ABC内任意一条直线垂直,证明你的结论.
⑶如果在折成的三棱锥内有一个小球,求出球的半径的最大值.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省鄂州市高一(下)期末数学试卷(文理合卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com