
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
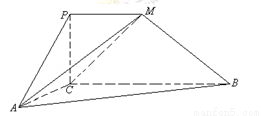
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
(1)详见解析;(2)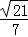 ;(3)
;(3)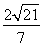
【解析】
试题分析:(1)先根据线面垂直的判定定理证PC⊥平面ABC,即可证得PC⊥AC。(2)用空间向量法求二面角。先过C作BC的垂线,建立空间直角坐标系,再求各点的坐标,和各向量的坐标,再根据向量垂直的数量积公式求面的法向量,但需注意两法向量所成的角和二面角相等或互补。(3)在(2)中已求出面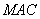 的一个法向量
的一个法向量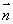 ,根据
,根据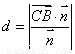 可求其距离。
可求其距离。
试题解析:【解析】
(1)证明:∵PC⊥BC,PC⊥AB, ∴PC⊥平面ABC,∵
∴PC⊥平面ABC,∵ ∴PC⊥AC. 2分
∴PC⊥AC. 2分
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.
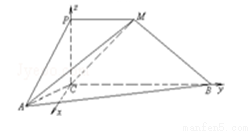
设P(0,0,z),则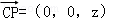 .
.
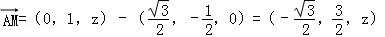 .
.
∵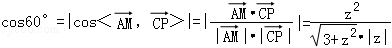 ,
,
且z>0,∴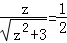 ,得z=1,∴
,得z=1,∴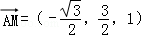 .
.
设平面MAC的一个法向量为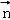 =(x,y,1),则由
=(x,y,1),则由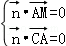
得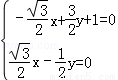 得
得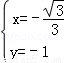 ∴
∴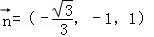 .
.
平面ABC的一个法向量为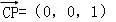 .
.
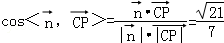 .
.
显然,二面角M﹣AC﹣B为锐二面角,∴二面角M﹣AC﹣B的余弦值为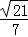 . 8分
. 8分
(3)点B到平面MAC的距离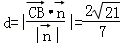 . 12分
. 12分
考点:1线线垂直、线面垂直;2空间向量法解决立体几何问题。


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
若随机变量X~B(100,p),X的数学期望E(X)=24,则p的值是( )
(A) (B)
(B) (C)
(C)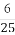 (D)
(D)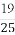
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取出了ξ个白球,下列概率等于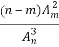 的是( )
的是( )
(A)P(ξ=3) (B)P(ξ≥2)
(C)P(ξ≤3) (D)P(ξ=2)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数
(1)若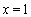 为
为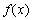 的极值点,求
的极值点,求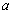 的值;
的值;
(2)若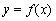 的图象在点
的图象在点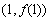 处的切线方程为
处的切线方程为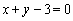 ,
,
①求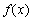 在区间
在区间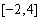 上的最大值;
上的最大值;
②求函数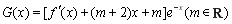 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知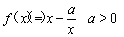 ,
,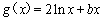 ,且直线
,且直线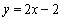 与曲线
与曲线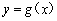 相切.
相切.
(1)若对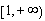 内的一切实数
内的一切实数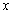 ,不等式
,不等式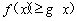 恒成立,求实数
恒成立,求实数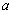 的取值范围;
的取值范围;
(2)当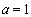 时,求最大的正整数
时,求最大的正整数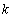 ,使得对
,使得对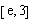 (
(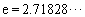 是自然对数的底数)内的任意
是自然对数的底数)内的任意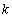 个实数
个实数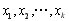 都有
都有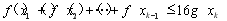 成立;
成立;
(3)求证: .
.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:填空题
已知函数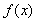 =x+sinx.项数为19的等差数列
=x+sinx.项数为19的等差数列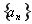 满足
满足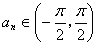 ,且公差
,且公差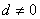 .若
.若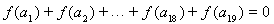 ,则当
,则当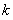 =__________时,
=__________时,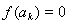 .
.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
已知A={x|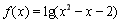 ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|<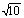 ,i为虚数单位,x>0},则A
,i为虚数单位,x>0},则A B=( )
B=( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
一次射击训练,某小组的成绩只有7环、8环、9环三种情况,且该小组的平均成绩为8.15环,设该小组成绩为7环的有x人,成绩为8环、9环的人数情况见下表:
环数(环) | 8 | 9 |
人数(人) | 7 | 8 |
那么x=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com