【题目】已知cosx=﹣ 
，x∈（0，π）
（1）求cos（x﹣ 
）的值；
（2）求sin（2x+ 
）的值．
【答案】
（1）解：∵cosx=﹣ 
，x∈（0，π）
∴sinx= 
= 
，
∴cos（x﹣ 
）= 
×（﹣ ）+ × = 
．
（2）解：由（1）可得：sin2x=2sinxcosx=2× 
=﹣ 
，
cos2x=2cos2x﹣1=2× 
﹣1=﹣ 
，
∴sin（2x+ 
）= 
sin2x+ 
cos2x= 
（﹣ ）+ ×（﹣ ）=﹣ 
【解析】（1）由已知利用同角三角函数基本关系式可求sinx的值，利用两角差的余弦函数公式及特殊角的三角函数值即可计算得解cos（x﹣ ）的值．（2）由（1）利用二倍角公式可得sin2x，cos2x的值，利用两角和的正弦函数公式，特殊角的三角函数值即可计算得解sin（2x+ ）的值．
轻松课堂单元期中期末专题冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】从某校高二年级学生中随机抽取了20名学生，将他们的期中考试数学成绩(满分100分，成绩均为不低于40分的整数)分成六段：[40，50)，[50，60)，…，[90，100]后得到如图所示的频率分布直方图．
求图中实数a的值；
若该校高二年级共有学生600名，试估计该校高二年级期中考试数学成绩不低于60分的人数；
若从数学成绩在[60，70)与[90，100]两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值大于10的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直三棱柱
中， 
是等腰直角三角形， 
，侧棱
， 
分别为
与
的中点，点
在平面
上的射影是
的重心.
（1）求证： 
平面
；
（2）求
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10 m到位置D，测得∠BDC＝45°，则塔AB的高是（ ）
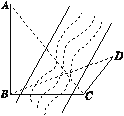
A. 10m B. 10
m C. 10
m D. 10
m
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，曲线
： 
（
为参数），以坐标原点
为极点， 
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
，直线
的极坐标方程为
．
（Ⅰ）分别求曲线
的极坐标方程和曲线
的直角坐标方程；
（Ⅱ）设直线
交曲线
于
， 
两点，交曲线
于
， 
两点，求
的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图：
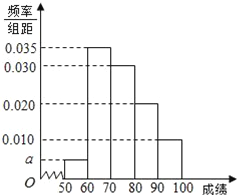
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知{an}为等差数列，且a3=﹣6，a6=0．
（1）求{an}的通项公式．
（2）若等比数列{bn}满足b1=8，b2=a1+a2+a3 ， 求{bn}的前n项和公式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
