
【题目】已知f(x)=2sin(x-![]() )-
)-![]() ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)判断函数![]() 在
在![]() 和
和![]() 的单调性,并用定义证明
的单调性,并用定义证明![]() 在
在![]() 上的单调性;
上的单调性;
(2)若函数![]() 是定义域为
是定义域为![]() 的偶函数,且
的偶函数,且![]() 时,
时, ![]() ,
,
①当![]() 时,写出
时,写出![]() 的表达式;
的表达式;
②若函数![]() 有四个零点,写出
有四个零点,写出![]() 的取值范围(不需要说明理由).
的取值范围(不需要说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:
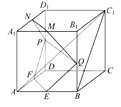
(1)直线BC1∥平面EFPQ.
(2)直线AC1⊥平面PQMN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女 | 16 | ||
男 | 14 | ||
合计 | 30 |
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查在![]() 级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
(1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为![]() 级风的海上航行中晕船与性别有关?
级风的海上航行中晕船与性别有关?
晕船 | 不晕船 | 总计 | |
男人 | |||
女人 | |||
总计 |
附:.![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com