
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,给人们带来新的出行体验,某共享单车运营公司的市场研究人员为了了解公司的经营状况,对公司最近6个月的市场占有率![]() 进行了统计,结果如下表:
进行了统计,结果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)请用相关系数说明能否用线性回归模型拟合![]() 与月份代码
与月份代码![]() 之间的关系.如果能,请计算出
之间的关系.如果能,请计算出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)根据调研数据,公司决定再采购一批单车扩大市场,从成本1000元/辆的![]() 型车和800元/辆的
型车和800元/辆的![]() 型车中选购一种,两款单车使用寿命频数如下表:
型车中选购一种,两款单车使用寿命频数如下表:
| 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年能为公司带来500元的收入,不考虑除采购成本以外的其它成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,以平均每辆单车所产生的利润的估计值为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数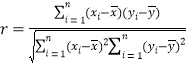 ,
, ,
,![]() .
.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
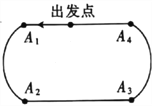
(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题其中正确的有( )
A.“实数都大于0”的否定是“实数都小于或等于0”
B.“三角形外角和为360度”是含有全称量词的真命题
C.“至少存在一个实数![]() ,使得
,使得![]() ”是含有存在量词的真命题
”是含有存在量词的真命题
D.“能被3整除的整数,其各位数字之和也能被3整除”是全称量词命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的口袋中装有大小、形状完全相同的![]() 个小球,将它们分别编号为
个小球,将它们分别编号为![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,甲、乙、丙三人从口袋中依次各抽出
,甲、乙、丙三人从口袋中依次各抽出![]() 个小球.甲说:我抽到了编号为
个小球.甲说:我抽到了编号为![]() 的小球,乙说:我抽到了编号为
的小球,乙说:我抽到了编号为![]() 的小球,丙说:我没有抽到编号为
的小球,丙说:我没有抽到编号为![]() 的小球.已知甲、乙、丙三人抽到的
的小球.已知甲、乙、丙三人抽到的![]() 个小球的编号之和都相等,且甲、乙、丙三人的说法都正确,则丙抽到的
个小球的编号之和都相等,且甲、乙、丙三人的说法都正确,则丙抽到的![]() 个小球的编号分别为________________.
个小球的编号分别为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,
为常数,![]() ,且
,且![]() ),点
),点![]() (
(![]() 在
在![]() 轴下方)是曲线
轴下方)是曲线![]() 与
与![]() 的两个不同交点.
的两个不同交点.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
以这100台机器维修次数的频率代替1台机器维修次数发生的概率, 记![]() 表示1台机器三年内共需维修的次数,
表示1台机器三年内共需维修的次数,![]() 表示购买1台机器的同时购买的维修次数.
表示购买1台机器的同时购买的维修次数.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以在维修上所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成:①里程计费:1元/公里;②时间计费:![]() 元/分.已知陈先生的家离上班公司
元/分.已知陈先生的家离上班公司![]() 公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为
公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为![]() (分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示
(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示

将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为![]()
![]() 分.
分.
(1)估计陈先生一次租用新能源租赁汽车所用的时间不低于![]() 分钟的概率;
分钟的概率;
(2)若公司每月发放![]() 元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按
元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按![]() 天计算),并说明理由.(同一时段,用该区间的中点值作代表)
天计算),并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com