
已知函数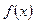 的定义域为
的定义域为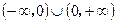 ,且满足条件:①
,且满足条件:①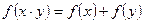 ,②
,②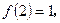 ③当
③当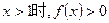 .
.
(1)求证:函数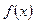 为偶函数;
为偶函数;
(2)讨论函数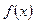 的单调性;
的单调性;
(3)求不等式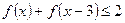 的解集
的解集
解:(1)在①中令x="y=1," 得f(1)= f(1)+ f(1)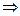 f(1)=0,
f(1)=0,
令x=y=-1, 得f(1)= f(-1 )+ f(-1)
)+ f(-1)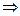 f(-1)=0,
f(-1)=0,
再令y=-1, 得f(-x)= f(x)+ f(-1)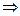 f(x), ∴f(x)为偶函 数;
f(x), ∴f(x)为偶函 数;
(2)在①中令
先讨论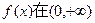 上的单调性, 任取x1http://www.zxxk.com/x2,设x2>x1>0,
上的单调性, 任取x1http://www.zxxk.com/x2,设x2>x1>0,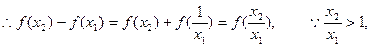
由③知: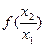 >0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数,
>0,∴f(x2)>f(x1), ∴f(x)在(0,+∞)上是增函数,
∵偶函数图象关于y轴对称 ,∴f(x)在(-∞,0)上是减函数;[来源:Z+xx+k.Com]
(3)∵f[x(x-3)]= f(x)+ f(x-3)≤2, 由①②得2=1+1= f(2)+ f(2)= f( 4)= f(-4),
4)= f(-4),
1)若x(x-3)>0 , ∵f(x)在(0,+∞)上为 增函数,
增函数,
由f[x(x-3)] ≤f(4) 得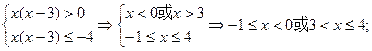
2)若x(x-3)<0 , ∵f(x)在(-∞,0)上为减函数;
, ∵f(x)在(-∞,0)上为减函数;
由f[x(x-3)] ≤f(-4)得 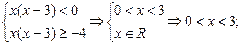
∴原不等式的解集为: 
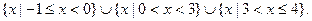
解析


科目:高中数学 来源: 题型:解答题
某自来水厂的蓄水池中有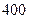 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时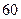 吨的速度向池中注水.已知
吨的速度向池中注水.已知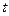 小时内向居民供水总量为
小时内向居民供水总量为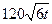 吨
吨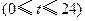 ,问
,问
(1)每天几点时蓄水池中的存水量最少?
(2)若池中存水量不多于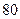 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分 ) .已知函数y=
) .已知函数y= f(x)=
f(x)=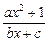 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<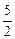
(1)试求函数f(x)的解析式
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说 明理由.
明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
(文科)已知二次函数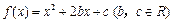 ,且
,且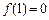 .
.
(1)若函数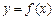 与x轴的两个交点
与x轴的两个交点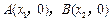 之间的距离为2,求b的值;
之间的距离为2,求b的值;
(2)若关于x的方程 的两个实数根分别在区间
的两个实数根分别在区间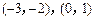 内,求b的取值范围.
内,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某微机培训机构打算购进一批微机桌和鼠标垫 ,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这
,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这 两家商场都给出了优惠条件
两家商场都给出了优惠条件
商场甲:买一赠一,买一张微机桌,赠一个鼠标垫
商场乙:打折,按总价的95%收款
该培训机构需要微机桌 60张,鼠标垫
60张,鼠标垫 个(
个(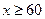 ),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?
),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com