
分析 复数z+i,$\frac{z}{2+i}$均为实数,可设z=x-i,$\frac{x-i}{2+i}$=$\frac{2x-1}{5}$-$\frac{2+x}{5}$i,可得-$\frac{2+x}{5}$=0,z=-2-i.在复平面内,(z+ai)2=4-(a-1)2-4(a-1)i的对应点在第四象限内,可得4-(a-1)2>0,-4(a-1)<0,解出即可得出.
解答 解:∵复数z+i,$\frac{z}{2+i}$均为实数,
设z=x-i,$\frac{x-i}{2+i}$=$\frac{(x-i)(2-i)}{(2+i)(2-i)}$=$\frac{2x-1}{5}$-$\frac{2+x}{5}$i,∴-$\frac{2+x}{5}$=0,
∴x=-2.
∴z=-2-i.
∵在复平面内,(z+ai)2=[-2+(a-1)i]2=4-(a-1)2-4(a-1)i的对应点在第四象限内,
∴4-(a-1)2>0,-4(a-1)<0,
解得:1<a<3.
∴实数a的取值范围是(1,3).
点评 本题考查了复数的运算法则、复数为实数的充要条件、几何意义,考查了推理能力与计算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
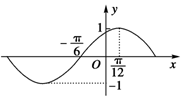
| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(2x+\frac{π}{6})$ | D. | $y=sin(2x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${({\sqrt{2}+\sqrt{7}})^2}<{({\sqrt{3}+\sqrt{6}})^2}$ | B. | ${({\sqrt{2}-\sqrt{6}})^2}<{({\sqrt{3}-\sqrt{7}})^2}$ | C. | ${({\sqrt{2}-\sqrt{3}})^2}<{({\sqrt{6}-\sqrt{7}})^2}$ | D. | ${({\sqrt{2}-\sqrt{3}-\sqrt{6}})^2}<{({-\sqrt{7}})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x+1>ex | B. | ?x∈R,x+1≥ex | C. | ?x∈R,x+1≥ex | D. | ?x∈R,x+1>ex |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com