
【题目】“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有菱草垛、方垛、刍童垛、三角垛等等,某仓库中部分货物堆放成如图所示的“菱草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是n件,已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的![]() .若这堆货物总价是
.若这堆货物总价是![]() 万元,则n的值为( )
万元,则n的值为( )
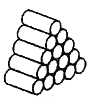
A. 7B. 8C. 9D. 10
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走了几个单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到起点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )
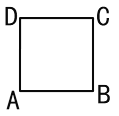
A.21种B.22种C.25种D.27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 给出下列4个命题:①当且仅当
给出下列4个命题:①当且仅当![]() 时,
时,![]() 是偶函数;②函数
是偶函数;②函数![]() 一定存在零点;③函数在区间
一定存在零点;③函数在区间![]() 上单调递减;④当
上单调递减;④当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,那么所有真命题的序号是_______.
,那么所有真命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
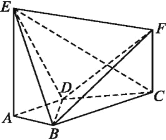
(1)求证:BF∥平面ADE;
(2)若二面角E-BD-F的余弦值为![]() ,求线段CF的长.
,求线段CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com