
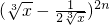 展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.
展开式中偶数项二项式系数的和比(1+x)n展开式的各项系数和大112.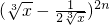 展开式中的所有的有理项.
展开式中的所有的有理项. (-x)4=70x4. …(8分)
(-x)4=70x4. …(8分) •
•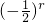 •
•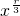 =
=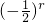 •
• •
• ,∴
,∴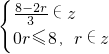 .
.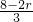 =k 则,r=4-
=k 则,r=4- k,∴k=-2,0,2,即 r=1,4,7.
k,∴k=-2,0,2,即 r=1,4,7.
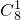 •x2=-4x2,T5=
•x2=-4x2,T5= •
• •x0=
•x0=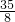 ,
,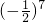 •
•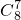 •x-2.…..13 分
•x-2.…..13 分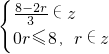 ,求得r=1,4,7,从而得到展开式中的所有的有理项.
,求得r=1,4,7,从而得到展开式中的所有的有理项.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com