
已知函数
(1)若函数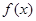 在点
在点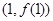 处的切线与圆
处的切线与圆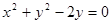 相切,求
相切,求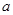 的值;
的值;
(2)当 时,函数
时,函数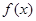 的图像恒在坐标轴
的图像恒在坐标轴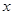 轴的上方,试求出
轴的上方,试求出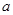 的取值范围.
的取值范围.
(1) ;(2)
;(2)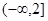 .
.
解析试题分析:本题综合考查函数与导数及运用导数研究函数的单调区间、最值等数学知识和方法,突出考查综合运用数学知识和方法分析问题、解决问题的能力,考查函数思想、分类讨论思想.第一问,先将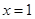 代入
代入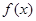 中,得到切点的纵坐标,对
中,得到切点的纵坐标,对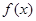 求导,将
求导,将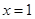 代入得到切线的斜率,所以点斜式写出切线方程,因为它与圆相切,所以圆心到切线的距离等于半径,列出表达式,求出
代入得到切线的斜率,所以点斜式写出切线方程,因为它与圆相切,所以圆心到切线的距离等于半径,列出表达式,求出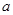 ;第二问,对
;第二问,对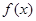 求导,通过分析可转化为当
求导,通过分析可转化为当 时,
时,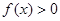 恒成立,设
恒成立,设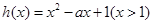 ,讨论
,讨论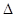 ,讨论
,讨论 的正负,通过抛物线的性质,求最小值.
的正负,通过抛物线的性质,求最小值.
试题解析:(1) 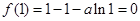 ,而
,而 ,故
,故 ,
,
所以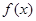 在点
在点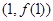 处的切线方程为
处的切线方程为 ,即
,即 ,
,
由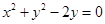 ,配方得
,配方得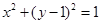 ,故该圆的圆心为
,故该圆的圆心为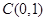 ,半径
,半径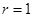 ,
,
由题意可知,圆 与直线
与直线 相切,所以
相切,所以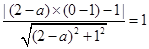 ,
,
即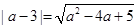 ,解得
,解得 . (4分)
. (4分)
(2)函数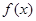 的定义域为
的定义域为 ,
, ,
,
由题意,只需当 时,
时,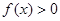 恒成立. (5分)
恒成立. (5分)
设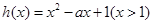 ,
,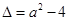 ,
,
当 时,
时, ,当
,当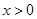 时,
时, 恒成立,即
恒成立,即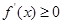 恒成立,
恒成立,
故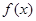 在
在 上是增函数,∴当
上是增函数,∴当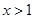 时,
时,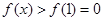 ,(7分)
,(7分)
当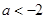 时,函数
时,函数 的对称轴
的对称轴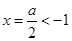 ,则
,则 在
在 上是增函数,
上是增函数,
当 时,
时,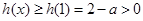 ,∴
,∴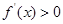 ,∴
,∴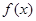 在
在 上是增函数,
上是增函数,
∴当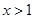 时,
时,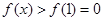 , (9分)
, (9分)
当 时,函数
时,函数 的对称轴
的对称轴 ,
, 在
在 是减函数,
是减函数,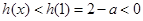 ,
,
故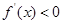 ,∴
,∴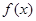 在
在 是减函数,
是减函数,
∴当 时,
时, 与当
与当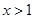 时,
时,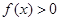 矛盾,(11分)
矛盾,(11分)
综上所述,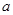 的取值范围是
的取值范围是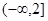 .
.
考点:1.利用导数求切线的方程;2.点到直线的距离公式;3.利用导数求函数最值.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
已知函数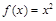 ,
,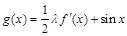 在
在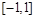 上的减函数.
上的减函数.
(Ⅰ)求曲线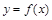 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;
(Ⅱ)若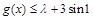 在
在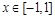 上恒成立,求
上恒成立,求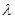 的取值范围;
的取值范围;
(Ⅲ)关于 的方程
的方程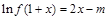 (
(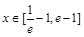 )有两个根(无理数e=2.71828),求m的取值范围.
)有两个根(无理数e=2.71828),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数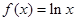 ,
,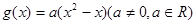 ,
,
(Ⅰ)若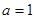 ,求函数
,求函数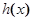 的极值;
的极值;
(Ⅱ)若函数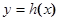 在
在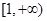 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(Ⅲ)在函数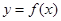 的图象上是否存在不同的两点
的图象上是否存在不同的两点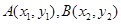 ,使线段
,使线段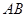 的中点的横坐标
的中点的横坐标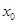 与直线
与直线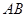 的斜率
的斜率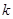 之间满足
之间满足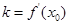 ?若存在,求出
?若存在,求出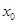 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数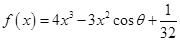 ,其中
,其中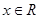 ,
,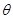 为参数,且
为参数,且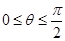 .
.
(1)当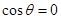 时,判断函数
时,判断函数 是否有极值;
是否有极值;
(2)要使函数 的极小值大于零,求参数
的极小值大于零,求参数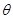 的取值范围;
的取值范围;
(3)若对(2)中所求的取值范围内的任意参数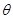 ,函数
,函数 在区间
在区间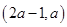 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量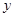 (单位:千套)与销售价格
(单位:千套)与销售价格 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式 ,其中
,其中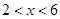 ,
, 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格 的值,使网校每日销售套题所获得的利润最大.(保留1位小数点)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com