
已知函数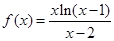 .
.
(Ⅰ)讨论函数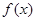 的单调性;
的单调性;
(Ⅱ)设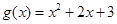 ,证明:对任意
,证明:对任意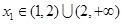 ,总存在
,总存在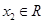 ,使得
,使得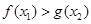 .
.
(1)f(x)在(1,2)单调递减函数,f(x)在(2,+∞)单调递增函数;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、不等式等基础知识,考查函数思想、分类讨论思想,考查综合分析和解决问题的能力.第一问,先对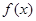 求导,而分子还比较复杂,所以对分子进行二次求导,导数非负,所以分子所对函数为增函数,而
求导,而分子还比较复杂,所以对分子进行二次求导,导数非负,所以分子所对函数为增函数,而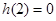 ,所以在
,所以在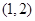 上
上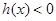 ,在
,在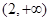 上
上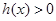 ,所以
,所以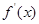 在
在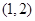 为负值,在
为负值,在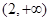 上为正值,所以得出
上为正值,所以得出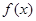 的单调性;第二问,先对已知进行转化,转化为
的单调性;第二问,先对已知进行转化,转化为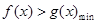 恒成立,而
恒成立,而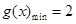 ,即转化为
,即转化为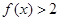 恒成立,再次转化为
恒成立,再次转化为 ,通过求导判断函数的单调性,判断
,通过求导判断函数的单调性,判断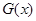 的正负.
的正负.
试题解析:(1)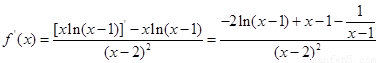 1分
1分
设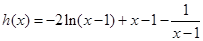 ,
,
∴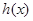 在
在 是增函数,又
是增函数,又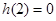 3分
3分
∴当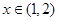 时,
时, 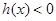 ,则
,则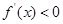 ,
,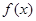 是单调递减函数;
是单调递减函数;
当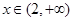 时,
时, 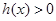 ,则
,则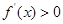 ,
,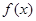 是单调递增函数.
是单调递增函数.
综上知: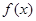 在
在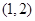 单调递减函数,
单调递减函数,
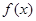 在
在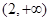 单调递增函数
6分
单调递增函数
6分
(2)对任意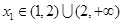 ,总存在
,总存在 ,使得
,使得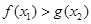 恒成立
恒成立
等价于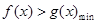 恒成立,而
恒成立,而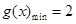 ,即证
,即证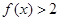 恒成立.等价于
恒成立.等价于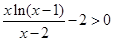 ,
,
也就是证 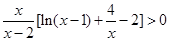 8分
8分
设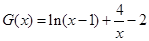 ,
, 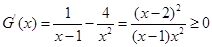 10分
10分
∴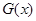 在
在 单调递增函数,又
单调递增函数,又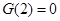
∴当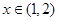 时,
时,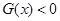 ,则
,则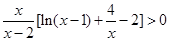
当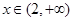 时,
时,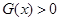 ,则
,则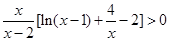
综上可得:对任意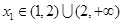 ,总存在
,总存在 ,
,
使得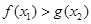 .
12分
.
12分
考点:1.利用导数判断函数的单调性;2.恒成立问题.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com