
【题目】已知椭圆E: ![]() =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
(1)求椭圆E的标准方程;
(2)证明:直线PQ与直线OQ的斜率之积是定值;
(3)证明:直线PQ与椭圆E只有一个公共点.
【答案】
(1)解:由题意可得 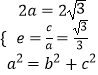 ,解得
,解得 ![]() ,c=1,
,c=1, ![]()
所以椭圆E: ![]() .
.
(2)解:由(1)可知:椭圆的右准线方程为 ![]() ,
,
设P(3,y0),Q(x1,y1),
因为PF2⊥F2Q,所以 ![]() ,
,
所以﹣y1y0=2(x1﹣1)
又因为 ![]() 且
且 ![]() 代入化简得
代入化简得 ![]() .
.
即直线PQ与直线OQ的斜率之积是定值 ![]()
(3)解:由(2)知, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴直线PQ的方程为 ![]() ,即
,即 ![]() ,
,
联立 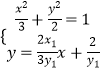 得
得 ![]() ,
,
∵ ![]() ,
, ![]() .
.
∴化简得: ![]() ,又△=0,
,又△=0,
解得x=x1,所以直线PQ与椭圆C相切,只有一个交点
【解析】(1)由题意可得 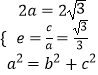 ,解出即可;(2)由(1)可知:椭圆的右准线方程为
,解出即可;(2)由(1)可知:椭圆的右准线方程为 ![]() ,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得
,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得 ![]() ,利用斜率计算公式可得kPQkOQ及
,利用斜率计算公式可得kPQkOQ及 ![]() 代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为
代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为 ![]() ,即
,即 ![]() ,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
【考点精析】关于本题考查的直线的斜率和椭圆的标准方程,需要了解一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是 ![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1 , CC1上,且C1F= ![]() C1C,BE=λBB1 , 0<λ<1.
C1C,BE=λBB1 , 0<λ<1. 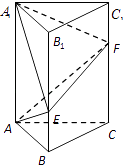
(1)当λ= ![]() 时,求异面直线AE与A1F所成角的大小;
时,求异面直线AE与A1F所成角的大小;
(2)当直线AA1与平面AEF所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
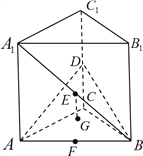
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论: ①函数 ![]() 的值域是(0,+∞);
的值域是(0,+∞);
②直线2x+ay﹣1=0与直线(a﹣1)x﹣ay﹣1=0平行,则a=﹣1;
③过点A(1,2)且在坐标轴上的截距相等的直线的方程为x+y=3;
④若圆柱的底面直径与高都等于球的直径,则圆柱的侧面积等于球的表面积.
其中正确的结论序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com