
【题目】已知![]() 是抛物线
是抛物线![]() :
: ![]() (
(![]() )上一点,
)上一点, ![]() 是抛物线的焦点,
是抛物线的焦点, ![]() 且
且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,以
两点,以![]() 为圆心的圆
为圆心的圆![]() 与直线
与直线![]() 相切,试判断圆
相切,试判断圆![]() 与直线
与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】(1)抛物线![]() 的方程为
的方程为![]() ;(2)圆
;(2)圆![]() 与直线
与直线![]() 相切.
相切.
【解析】试题分析:(1)由抛物线![]() 的方程,可得焦点坐标与准线方程
的方程,可得焦点坐标与准线方程![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
连接![]() ,利用等边三角形,求得
,利用等边三角形,求得![]() 的值,即可得到抛物线的方程;
的值,即可得到抛物线的方程;
(2)当直线![]() 的斜率不存在时,可得圆
的斜率不存在时,可得圆![]() 与直线
与直线![]() 相切.
相切.
当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,代入抛物线的方程,求得
,代入抛物线的方程,求得![]() ,进而得到直线
,进而得到直线![]() 、
、![]() 的方程,求得点
的方程,求得点![]() 到直线
到直线![]() 的距离,得到
的距离,得到![]() ,即可判定直线与圆相切.
,即可判定直线与圆相切.
试题解析:
(1)抛物线![]() :
: ![]() (
(![]() )的准线方程为
)的准线方程为![]() :
: ![]() ,
,
过![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() 为等边三角形,
为等边三角形,
∴![]() ,∴
,∴![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)直线![]() 的斜率不存在时,
的斜率不存在时, ![]() 为等腰三角形,且
为等腰三角形,且![]() .
.
∴圆![]() 与直线
与直线![]() 相切.
相切.
直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,
,
代入抛物线方程,得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴圆![]() 的半径
的半径![]() 满足
满足
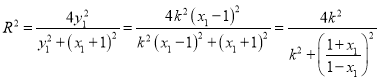 .
.
同理,直线![]() 的方程为
的方程为![]() ,
,
![]() 到直线
到直线![]() 的距离
的距离![]() ,
, 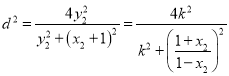
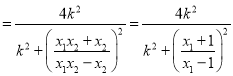 .
.
∴![]() ,∴
,∴![]() ,∴圆
,∴圆![]() 与直线
与直线![]() 相切,
相切,
综上所述,圆![]() 与直线
与直线![]() 相切.
相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: 
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上,社区最近四年内在“文化丹青”上的投资金额统计数据如表: (为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(Ⅰ)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ) 预测该社区在2019年在“文化丹青”上的投资金额.
附:对于一组数据![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为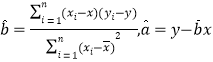 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 向左平移
向左平移![]() 个单位长度后得到
个单位长度后得到![]() ,
,![]() 到
到![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com